體積比對靜態(tài)膨脹法真空系統(tǒng)不確定度的影響
要使靜態(tài)膨脹法真空系統(tǒng)測量不確定度達到10-3,體積比的測量是最關(guān)鍵的一步,墨西哥CENAM的體積比不確定度可以達到3×10-4 。
表1 不同路徑對應(yīng)的體積比
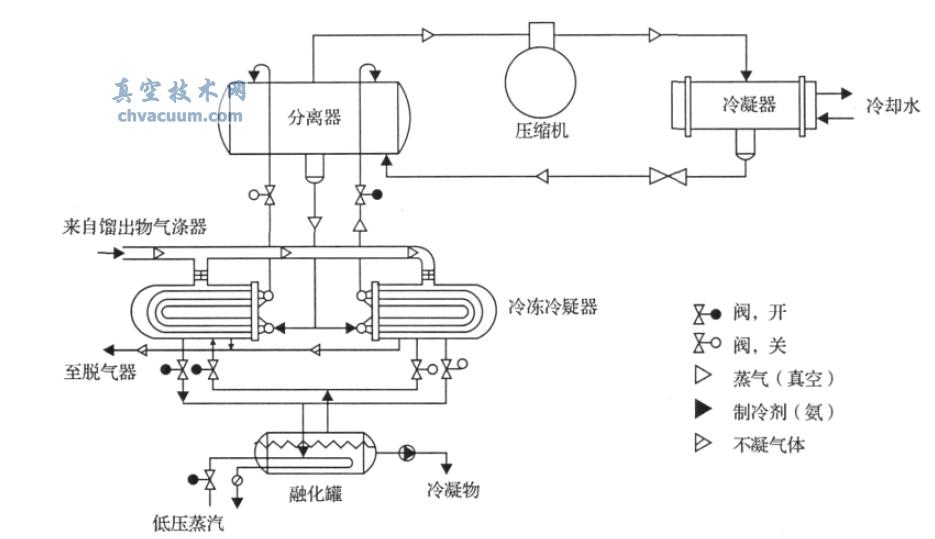
氣體通過不同容積的小體積向大體積膨脹,可以獲得不同體積比:通過v1或v2向大體積V1膨脹,以及v3向V2膨脹,分別得到10-2或10-3的壓降率,不同的膨脹路徑得到的體積比如表1所示。為了得到更大的壓降,我們采用在I 級膨脹室循環(huán)多次的方法,可得到從10-2到10-9一系列不同的體積比。前級壓力取樣范圍(104～105) Pa, 經(jīng)過不同路徑的膨脹,可得到(10-4～103) Pa的不同測量值。為了確定體積比值,我們采用灌水稱重法來獲得小體積的容積值,采用參考體積法來獲得大體積的容積值。
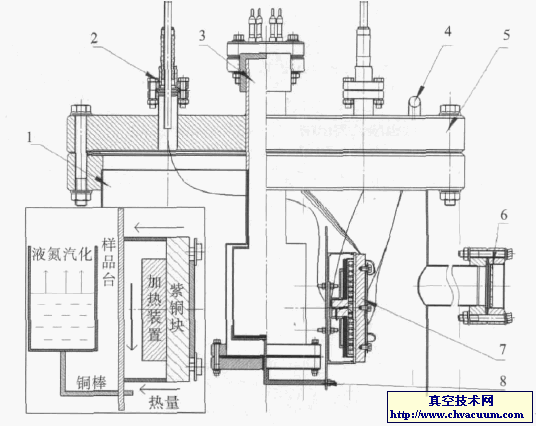
灌水稱重法是一種絕對的測量容積值的方法,分別測量容器灌水前后的質(zhì)量,通過計算質(zhì)量差和水密度來得到容積值。稱重使用的是分辨力為10mg的天平,用替代法稱出小體積灌水前后質(zhì)量,并同時測量實驗室空氣密度,進行空氣浮力修正。用精度為0.01 ℃的溫度計測量水溫,得到相應(yīng)水密度。用灌水稱重法測得小體積容積結(jié)果為:
v1=0.772946L u ( v1)=2.1 ×10-5
v2=0.074663L u ( v1) =7.7 ×10-5
v3=0.752388L u ( v1) =3.3 ×10-5
稱重法測體積在原理上可達到很小的不確定度,但由于大體積上連接很多管路和閥門,形狀復(fù)雜,死角很多,灌水后很難使氣泡排盡,復(fù)雜的結(jié)構(gòu)也會使水溫分布趨于復(fù)雜,這就是大體積用直接稱重法的測量不確定度并不很小的根本原因。
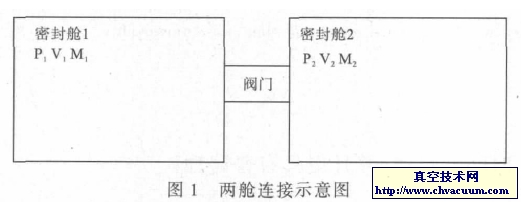
例如PTB于1969年對約233升的大體積進行灌水的稱重測量,其過程十分繁復(fù),即使如此,測量不確定度也不過55mL, 即相對不確定度為2.3 ×10-4 。為了解決大體積的測量問題,我們設(shè)計了參考體積———約為大體積容積的1/4, 但結(jié)構(gòu)單一且內(nèi)表面光滑無死角,用灌水稱重法測量參考體積的容積值,其相對標準偏差可以達到1 ×10-5 。再用參考體積通過單次膨脹的壓力比法測出大體積的容積值,由于參考體積與大體積容積在同一量級,我們采用石英壓力計的精確范圍來進行壓力測量,參考體積與大體積比值多次測量的相對標準偏差小于4 ×10-5 。用這種方法不僅能夠解決大體積的測量問題,還易于今后大體積復(fù)測。大體積經(jīng)換算和修正后,結(jié)果如下:
V1=82.9075L u(V1) =2.1×10-4
V2=82.2713L u(V2) =2.1×10-4
為了驗證體積比測量的準確性,也為了找出大體積可能的系統(tǒng)差,我們對目前常用的累積法做了改進。由于累積法每次測量耗時長,且前10次膨脹不計入,所以我們提出了增量法和預(yù)壓累積法,分別對1∶100和1∶1000的體積比進行了復(fù)測,測量結(jié)果如表2 所示。
表2 不同測量方法得到的體積比
用增量法多次測量1∶100體積比,達到的相對標準差約為1 ×10-4 ;用預(yù)壓累積法測量1∶1000體積比,達到的相對標準差約為6 ×10-4 。不同方法測得體積比結(jié)果的相對偏差為10-4量級,說明這幾種測量方法是準確可靠的,也可以將增量法或預(yù)壓累積法用于今后的體積比復(fù)現(xiàn)。
其它相關(guān)文章：
