為了實現電動執行器在精確性、靈敏度、快速反應和穩定性等方面，將基于矢量控制策略應用于電動執行機構。采用矢量控制方法，可實現優良的控制品質。并根據矢量控制理論設計出的新型電動行機構，仿真和實踐結果表明：具有良好的動靜態特性。

1、引言

　　電動執行機構在控制系統中又稱為終端控制元件，是自動控制系統中不可缺少的重要組成部分。它是利用電源為動力并在某種控制信號作用下工作，能提供直線或旋轉運動的驅動裝置。

2、矢量控制策略

2.1、矢量控制理論的提出和坐標變換

　　矢量控制在國際上一般多稱為磁場定向控制(FieldOrientation)，亦即把磁場矢量的方向作為坐標軸的基準方向，電動機電流矢量的大小、方向均用瞬時值來表示。1971年，由德國西門子公司的Blaschke等人將這種一般化的概念形成系統的交流電動機的矢量控制(TransvectorContrl)理論，從理論上解決了交流電動機轉矩的高性能控制問題。矢量控制理論的基本思想是在三相交流電動機上模擬直流電動機轉矩控制的規律。通常在磁場定向坐標上，三相繞組在空間位置上互差3π/2rad機械角度，設在三相繞組中通以三相對稱電流，在相位上互差3π/2rad電角度，產生的合成磁場具有以下特點：

　　(1)隨著時間的推移，合成磁場的軸線在旋轉，電流交變一個周期，磁場也將旋轉一周;

　　(2)在旋轉過程中，合成磁場強度不變，故稱圓形旋轉磁場。

　　考慮兩相對稱繞組，其在空間位置上互相“垂直”，互差3π/2rad電角度;兩相交變電流在相位上互差3π/2rad電角度。將兩相對稱電流通入兩相對稱繞組，產生的合成磁場將具有與三相旋轉磁場同樣的特性。如果在旋轉體R上放置2個匝數相等、互相垂直的直線繞組M和T，如圖1所示。

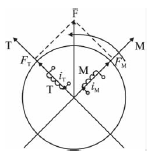
圖1 兩相直流旋轉繞組示意圖

　　則當2個繞組內分別通入直流電流iM和iT時，它們的合成磁場仍然是恒定磁場。如果調節任何一個直流電流(iM或iT)，則合成磁場的磁場強度也得到了調整。當R旋轉時，兩繞組同時以同步轉速旋轉，合成磁動勢產生的合成磁通也會旋轉，此恒定磁場將子空間形成一個機械旋轉磁場，它與前面介紹的三相、兩相繞組產生的磁場完全可以等效。當觀察者站到鐵心上和繞組一起旋轉時，看到的將是2個通以直流的、相互垂直的固定繞組。如果采取補償措施補償掉繞組T產生的磁動勢FT，電動機的主磁通只由M繞組產生，并和iM成正比。而T繞組中電流iT和磁場Φ作用將產生旋轉，其大小只與電流iT成正比，這與直流電動機轉矩產生的原理非常相似，得到在靜動態性能上完全能夠與直流調速系統相媲美的交流調速系統。因此，必須對電動機的參考坐標系進行變換。

2.2、矢量控制的實現

　　在研究矢量控制時，定義有三種坐標系統，即從三相到兩相的靜止坐標變換(3s/2s變換)和從兩相靜止到兩相旋轉地坐標變換(2s/2r變換)。

　　一個旋轉矢量i從三相定子A-B-C坐標系變換到兩相定子α-β坐標系，稱為Clarke變換，也叫作3s/2s變換，其矩陣形式為式(1)：

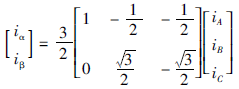
　　其原理示意圖如圖2所示。

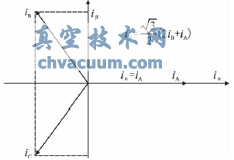
圖2 CLARKE變換示意圖

　　其逆變換，即Clarke逆變換或2/3變換矩陣式為式(2)：

　　一個旋轉矢量i從d-q垂直坐標系變換到M-T定向坐標系，稱為Park變換，也叫作交/直變換，其矩陣形式為式(3)：

　　其變換原理圖如圖3所示。

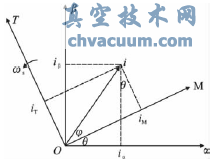
圖3 PARK變換示意圖

　　其逆變換，即Park逆變換或直/交變換的矩陣形式為式(4)：

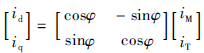
3、系統的基本方程式和結構框圖

　　下面給出異步電動機兩相以同步速旋轉，按轉子磁場定向的M、T坐標的數學模型。

　　(1)電壓方程

　　(2)磁鏈方程

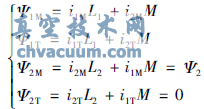
　　(4)電磁轉矩方程

　　以上各式中，r1、r2為定轉子電阻;L1、L2為定轉子自感;M為定轉子互感;u1M、u1T、u2M、u2T為M、T軸定轉子電壓;ωs為轉差角頻率;ω1為同步旋轉角頻率;T為電磁轉矩;i1M、i1T、i2M、i2T為M、T軸定轉子電流;PN為電動機極對數;Ψ1M、Ψ1T、Ψ2M、Ψ2T為M、T軸定轉子磁鏈;P為微分算子;Ψ2為轉子磁鏈。

　　交流異步電動機變頻調速矢量控制系統的結構框圖如圖4所示。圖中有上標的控制量為指令值，其余為實際值。首先將角速度指令ω*和ω的偏差信號e送入速度調節器，其輸出即為T*指令。由上面的矢量控制基本方程式可求出T*、i*1M、i*1T、Ψ2、ωs。經過一系列坐標變換后，即可得到三相電流指令I*a、I*b、I*c。在電流調節部分，由電流指令和經霍爾式電流傳感器檢測出實時電流相比較的偏差送入電流調節器。將輸出信號送給IGBT逆變器達到變頻調速的目的。

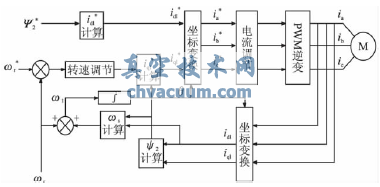
圖4 變頻調速矢量控制系統的結構框圖

4、基于MATLAB的變頻調速矢量控制的仿真

　　由上節推導的矢量控制系統的基本方程式，以及交流異步電動機變頻調速矢量控制系統的結構框圖，可得出在Simulink中的仿真結構圖，如圖5所示。

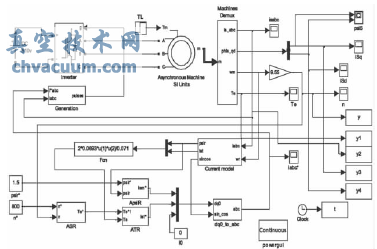
圖5 Simulink中的仿真結構圖

　　在Simulink的仿真結構圖中，系統速度調節器(ASR)的輸出信號是轉矩給定T*e。其內部構造為如圖6所示。其中轉矩限幅設為300，Kp設為12，Ki設為24。

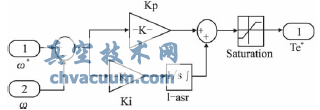
圖6 系統速度調節器子模塊

　　電流調節器(ACR)實現實際電流隨給定電流的變化，采用電流滯環控制原理來實現電流的調節。以A相為例，控制原理如圖7。將給定電流i*a與輸出電流ia進行比較，電流偏差△ia超過±h時，經滯環控制器HBC控制逆變器A相上(或下)橋臂的功率器件動作。B、C二相的原理圖均與此相同。

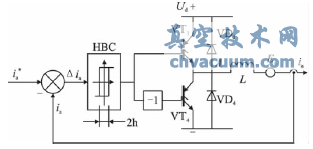
圖7 電流滯環控制的A相原理圖

　　其內部構造如圖8所示。

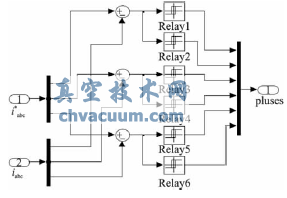
圖8 系統電流調節器子模塊

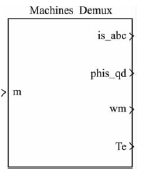
圖9 電機測試信號分配器

　　滯環寬度設為20。

　　在仿真過程中用到的電機測試信號分配器(Ma-chinesMeasurementDemux)，如圖9。在仿真過程中，選擇電動機轉速、電動機機械轉矩、三相定子電流和同步d-q坐標下的q軸下的定子磁通和d軸下的定子磁通為輸出信號。

　　異步電機參數：采用鼠籠式異步電動機，線電壓380V;額定頻率50Hz;定子內阻0.435Ω;定子漏感0.004mH;轉子內阻0.816Ω;轉子漏感0.004mH;互感34.7mH;極對數為4。仿真方法選擇為固定步長(fixed-step)。仿真時間設為0～1s。得到的電動機轉速、電動機機械轉矩、三相定子電流和同步d-q坐標下的q軸下的定子磁通和d軸下的定子磁通的響應曲線如圖10～14所示。

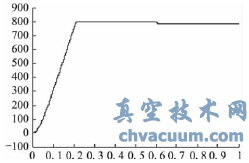
圖10 電動機轉速響應曲線

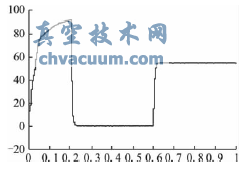
圖11 電動機機械轉矩響應曲線

圖12 三相定子電流曲線圖

圖13 q軸下的定子磁通響應曲線

圖14 d軸下的定子磁通響應曲線

4、結束語

　　本文從矢量控制的基本原理、異步電機的數學模型以及利用Matlab/Simulink工具出發，構造了矢量控制系統的仿真模型并仿真結果進行研究。研究結果表明，按轉子磁鏈定向的異步電動機矢量控制系統具有動態性能好、調速范圍寬的優點，且由以上實驗結果表明，仿真實現的矢量控制算法，在異步交流電機驅動的應用上，無論是控制電機的速度，還是控制位置，效果都很理想。