螺旋槽干氣密封動環模態分析及其模態特性試驗
針對大型核電設備的干氣密封裝置的振動特性的研究,利用ANSYS軟件對螺旋槽干氣密封動環模型進行自由模態分析和約束模態分析,計算得到其固有頻率和振型,為動環的動態響應分析提供參考;通過LMS振動試驗測試動環自由狀態下的固有頻率,將其結果與軟件計算結果相比較,通過其誤差大小可驗證軟件模態分析的可靠性。通過得到的固有頻率和振型結果對比分析,可知AN⁃SYS有限元分析結果是可信的,可根據分析結果對密封結構進行改善。
前言
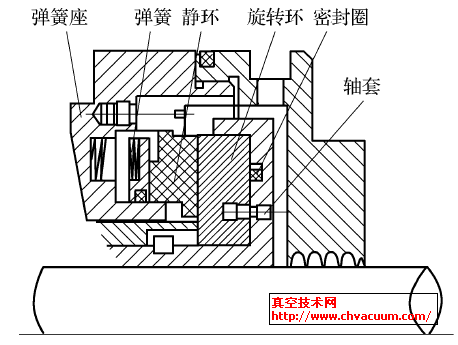
干氣密封是最常用的一種非接觸式密封方式之一,動環和靜環是這種密封結構的主要組成部分。當動環高速旋轉時,因流體靜壓和動壓作用,動靜環之間的密封環端面間會形成一層氣膜,同時產生一個開啟力使密封動靜環分離開來。非接觸式密封減少了密封環之間的摩擦,且氣膜相對比較穩定,可以減少泄漏量,減少磨損,提高密封性能和延長密封使用壽命,可靠性較高。
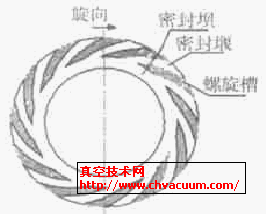
近年來,干氣密封被廣泛運用于多種壓縮機、泵及其他某些高速高壓設備中。目前,在該領域國內外都已經做了很多的研究,其中很多以密封端面的螺旋槽型作為研究對象,雖然從理論上來講,根據流體動力學知識,在干氣密封端面的溝槽無論是什么形狀,動環高速旋轉時,端面都會產生動壓效應,但蔡文新、王玉明等的理論研究表明,相比于其他槽型,螺旋槽密封工作時流體動壓效應更明顯,密封性能更好。
模態分析是動力學分析的基礎部分,它為動力學分析中的諧響應分析、譜分析以及瞬態動力學等分析打下了基礎,提供最基本的數據。需要分析的零件或結構的固有頻率和振型是模態分析計算的主要研究內容, 應用此分析得到所設計零部件的固有頻率和振型之后,就可以在工作中避開固有頻率值,預防由外界激勵而引起的共振,避免造成密封失效或者設備損害等后果。
基于此,本文以日機密封公司指定的一套螺旋槽干氣密封為研究對象,對其密封動環進行振動模態分析,并通過LMS振動試驗驗證分析的可靠性。
1、有限元模態分析
1)建立有限元模型
本文以日機密封的一個具體動環作為研究對象,首先利用SolidWorks對其進行三維建模,然后利用AN⁃SYS對其進行模態分析。其端面幾何尺寸為:內徑r1=101.25mm,外徑r2=131.5mm,螺旋槽底半徑r3=117mm。本文所用動環是一個軸對稱零件,用有限元方法分析計算時通常選擇四節點或八節點軸對稱單元。綜合考慮計算精度和效率等因素,最終選擇八節點六面體單元solid45來對此動環進行描述。動環的材料為SSiC,材料屬性為:彈性模量E=430 GPa;密度ρ=3240kg/m3;泊松比μ=0.26。利用有限元分析前處理專業軟件hypermesh 對動環三維模型進行網格劃分,生成103 858個單元和24 012個節點。螺旋槽動環模型如圖1所示。
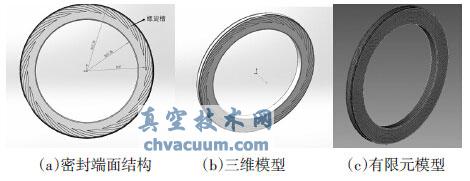
圖1 螺旋槽動環模型
2)確定邊界條件和求解方法
動環固定在軸套上,對動環外緣的3個約束面進行約束,同時受軸套、動環座、介質壓力和氣膜壓力的作用,工作時跟隨軸一起轉動。本文先對其進行自由模態分析,再進行約束模態分析。高速旋轉的零部件在工作時會受到離心力的作用,其固有頻率值與靜止時的值相比會存在一定的差異。因此,對動環進行模態分析時,設置邊界條件需要將離心力的影響列入考慮,故用ANSYS對其進行加預應力的模態分析,即在分析前加上動環527.52 rad/s的旋轉角速度。同時對動環的外部進行自由度約束。
在ANSYS將分析類型定義為模態分析后,需設置本次分析所關注的模態階數,并確定矩陣值求解方法。ANSYS常用的矩陣值求解法包括分塊蘭索斯法、子空間法、PowerDynamics法、縮減法等模態提取方法。對于對稱特征值求解問題,運用分塊蘭索斯法計算的收斂速度比其他的模態提取方法更快。為了計算速度比較快,且得到的結果也比較準確,本文采用分塊蘭索斯法。
3)模態分析結果
機械密封動環在運行過程中的振動會引起密封件磨損、變形等,從而導致密封效果不理想,若振動過大還會對整個機械密封結構的工作性能造成影響,甚至引起密封失效。模態是機械結構的固有特性,每一個模態對應相應的固有頻率、模態振型和阻尼比。然而不同的模態對結構頻率響應的貢獻是不同的,例如對本文中動環的低頻響應來說,高階模態的貢獻就較小。根據振動理論,此密封結構的動力學特性主要受低階模態的影響。故在實際應用中,只需研究結構的前幾階或十幾階模態,這樣工作量就大為減少。
2、結論
本文運用ANSYS對干起密封重要零件動環進行了有限元自由模態分析和約束模態分析,得到其前幾階固有頻率和振型。并對自由狀態下的動環進行了LMS動態特性試驗,得出了自由狀態下的前幾階固有頻率和振型,與之前的ANSYS計算結果相比較,可以看出誤差并不大,故ANSYS的計算結果是可信的。
通過ANSYS軟件對動環進行了加預應力的約束模態分析,選取了前8階固有頻率和振型作為研究對象,可以看出,此動環的前8 階固有頻率值在2661.3~10763HZ之間,在實際工作情況下,外界給予其振動頻率很難達到如此高的值,故可以認為動環在正常工作情況下不會發生共振,在以后的設計或優化過程中可以不用重點考慮振動對密封性能的影響,不過觀察動環振型可以看出,在約束位置上的變形最大,故為了使動環的振動對密封性能的影響更小,可以考慮在動環上多添加幾個約束面。