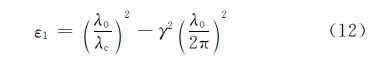根據微波材料的設計結構(如圓波導結構、非均勻加載結構)建立對應的模型，并以矢量網絡分析儀測量的S參數為基礎，通過HFSS仿真優化，最終給出相對應的相對復介電常數。由于傳統的測試平臺只能實現對微波材料樣品的測試，因此這里所述方法一方面對于縮短設計周期具有重要意義，另一方面避免了對復雜結構的特性阻抗及傳播常數繁瑣的求解過程。通過經典的NRW 算法所得結果與仿真所得結果相比較，驗證了該方法的有效性。

引言

　　微波材料的復介電常數與磁導率是其重要的電磁特性，在微波毫米波器件的研制中需要對其進行測量，從而在具體器件的設計過程中有效應用其特性實現相應的性能指標。微波材料的復介電常數有低損耗與高損耗之分，根據它們的特性需要設計相應的物理模型與實驗平臺來進行測試。在高功率毫米波真空器件中通過在波導或在諧振腔壁上加載損耗介質(微波介質材料)的方法，從而抑制其中的寄生模式，使振蕩器件或放大器件工作在單模狀態下，有效提高這些器件的工作效率、輸出功率與頻譜純度。同時介質加載對工作模式也會造成影響，所以需要對介質材料的介電常數進行有效的測定。在設計中通過對加載方式與材料的選取，一方面有效地抑制寄生模式，另一方面又使加載對工作模式的影響最小。國內現有的介質參數測試平臺只能實現對微波材料的樣品測試，為了縮短設計周期并提高測試精度需要建立跟相應的微波結構對應的測試平臺從而實現具體結構的直接測試。

1、理論分析

　　1.1、經典NRW 傳輸/反射法在矩形波導中，對于TE波，由于不含Ez分量，其橫向場分量可以由縱向場分量Hz來表示，而Hz滿足下面的波動方程及邊界條件：

　　由式(1)可求得TE波的其他橫向場分量：

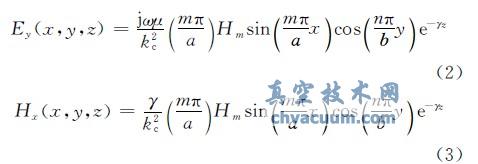
　　根據TE10場結構，定義“電壓”和“電流”分別為：

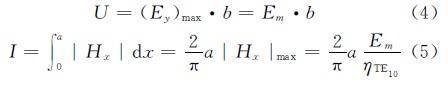
　　可得特性阻抗為(忽略了數字系數不同，假定為1)

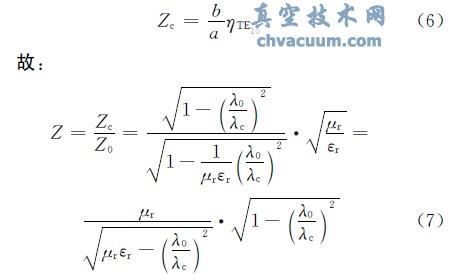
　　對于傳播常數：

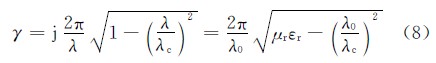
　　利用電磁場在介質左右邊界的縱向連續邊界條件，根據場匹配法建立起介質加載導致的行波反射與透射幅值與相位方程(對應于S11與S12參數)可得散射矩陣與歸一化矩陣的關系：

　　可以求得歸一化特征性阻抗Zc與傳播常數γ 的解析式：

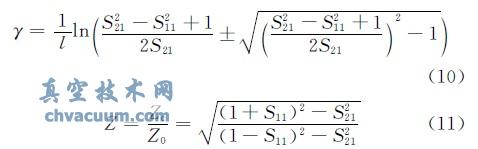
　　對任意樣品，由式(7)、(8)并結合式(10)、(11)可解出電磁參數εr，μr。而對于非磁性材料，μr =1，采用式(7)和式(8)聯合求解相對復介電常數值為：

　　若采用(3)式和(4)式求解的相對復介電常數值為：

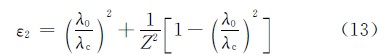
　　由于該實驗采用測試樣品厚度l=1mm，滿足厚度不大于波導波長的條件，故采用式(12)所得結果較為準確。

　　1.2、S 參數的測試及HFSS優化

　　本文的測試系統是通過矢量網絡分析儀來測試圓波導結構的S 參數，通過有效的抑制寄生模式，并采用如圖1所示的夾具使波導工作在TE11模式下，而測試夾具則通過同軸電纜與矢量網絡分析儀的兩個端口相連接。其測試結構尺寸為：Φ13.76×11.16×10。

圖1　TE11模夾具

　　在HFSS的環境下，建立如圖2所示的模型，將實測的S 參數設置為優化目標，將復介電常數設置為優化變量，通過反復的優化，使其誤差達到最小，取其對應的相對復介電常數為最終值。

圖2　TE11模式仿真模型

2、實驗結果及誤差分析

　　根據上述理論分析，在相同環境下，分別采用圓波導結構和矩形系統測試的結果如圖3和圖4所示。由圖可見，通過兩種系統測試所得的復介電常數實部均接近11，而損耗角正切接近0.8，且隨著頻率的增大有緩慢減小的趨勢，從而較好地驗證了采用具體結構直接測試材料復介電常數的可行性。

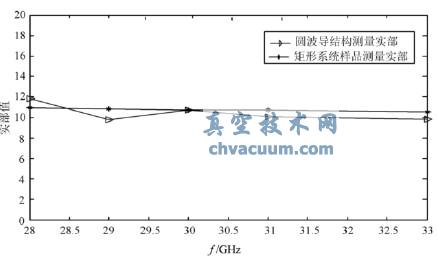
圖3　圓波導與矩形系統測試相對復介電常數實部對比

　　另一方面，通過兩組數據的對比可以發現，它們之間還是存在一定的誤差，特別是兩組數據的的實部之間。其相對誤差值如圖5所示。

　　分析其原因之一是NRW 方法本身存在一定的誤差，其誤差由下面的式子給出：

　　式中：Δε′，Δε″分別表示實部和虛部的絕對誤差;ε1和ε2表示由式(12)和式(13)計算出的結果。另一個原因是用矢量網絡分析儀測量的S 參數本身也存在一定的誤差，特別是S11相位對結果的影響較大，而實際測量中其值跳變也較大。而且通過HFSS軟件仿真優化一般情況下也并不能完全達到優化目標要求的值。

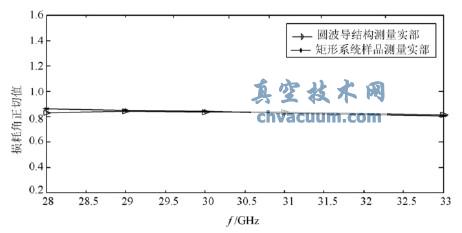
圖4　圓波導與矩形系統測試相對復介電常數損耗角正切對比

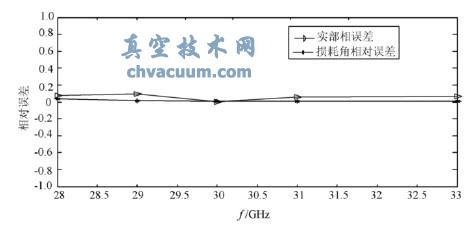
圖5　實部與損耗角正切相對誤差大小

3、結語

　　本文通過理論分析及實驗測量，給出了兩種不同系統下相同材料的復介電常數，通過它們之間的吻合驗證了直接測試圓波導結構復介電常數的有效性。從而對縮短實際生產中設計周期具有重要意義，也避免了對復雜結構的特性阻抗及傳播常數繁瑣的求解。最后，通過前人經驗及在實驗中遇到的問題對實驗誤差進行了有效的分析。