本文重點介紹了如何根據齒輪加工方式確定了齒槽的過渡曲線參數方程。為了實現各段曲線參數方程的連續性，根據齒輪的實際情況確定了各段曲線連接端點的取值范圍。并結合UG 軟件的相關特征操作實現斜齒輪的三維精確造型。

　　機械傳動中，漸開線斜齒輪的應用相當廣泛。由于齒廓曲線比較復雜，尤其是齒根部分的過渡曲線與齒輪的加工方式有關，所形成的過渡曲線也不一樣。為了得到齒廓曲線，必須通過數學模型來描述齒廓的各段曲線。

1、齒廓曲線的數學表達

　　斜齒輪端面齒廓曲線包括漸開線、齒根過渡曲線、齒根圓弧和齒頂圓弧。

　　1.1、齒廓漸開線的數學表達

　　斜齒輪端面漸開線的生成方法與直齒圓柱齒輪基本相同。不同之處在于斜齒輪法面模數mn、法面分度圓壓力角α、法面齒頂高系數h*an和法面頂隙端系數c*an為標準值，而齒廓曲線方程中用到的是端面壓力角αt與端面模數mt。建立圓的漸開線參數方程：

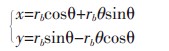
　　式中：rb為基圓的半徑;θ 為發生線與基圓的接觸點A 與B 之間所對應的圓心角。

　　1.2、齒廓過渡曲線的數學表達

　　過渡曲線與齒輪加工方式有關，但其原理基本相同。標準齒條刀具頂部比普通齒條多出一段c*m，用于被加工齒輪的齒根部分切出齒頂間隙。

　　現以齒條形刀具參數為例進行分析， 刀具齒廓的頂部有兩個圓角，Cp是圓角的圓心，圓角半徑等于rp。刀具各參數間具有以下關系：

　　式中：m 為齒條的模數;a 為點Cp至中線的距離;b 為點Cp至齒形中心線的距離;α 為齒條的壓力角也就是被加工齒輪的分度圓壓力角;h*a為齒頂高系數;c* 為頂隙系數;rp為圓角半徑。

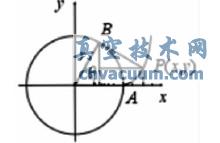
圖1 漸開線的形成

　　被加工齒輪齒廓的漸開線部分由刀具的斜直線部分切出，而齒根過渡曲線則由刀具的圓角部分切出。如圖2 所示，加工過程中刀具的加工節線與齒輪的節圓相切純滾， 刀具圓角的圓心將形成延伸漸開線，因此齒輪的過渡曲線是該延伸漸開線的等距曲線。P 點是節點，nn是刀具圓角與過渡曲線接觸點的公法線，可求得延伸漸開線等距曲線，即齒根過渡曲線的參數方程為：齒根過渡曲線的參數方程為：

　　式中：α' 為公法線與刀具加工節線間的夾角;r 為齒輪分度圓半徑;φ 為角度參變量。

　　由于刀具的圓角部分和與其連接的兩段直線相切，所以當刀具圓角與齒根過渡曲線剛開始接觸時，M 垂直于刀具的齒側直線，此時nn與嚙合線重合，α' 等于齒條與齒輪的分度圓壓力角α; 當齒條齒輪轉動到α'=π/2 時， 齒條形刀具的頂部直線段與齒根過渡曲線末端接觸，然后由該段直線切出齒根圓弧。由此可知，α'∈[α，π/2]。

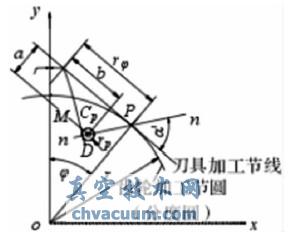
圖2 齒根過渡曲線

　　2.3、實現

　　斜齒輪的造型實現要求齒輪能夠實現在其設計要求發生改變時，它的結構尺寸也相應地改變以滿足新的設計需要。為此，只需要將上述所建立的齒輪實體模型的相關特征參數進行更改，就可以生成各種相關參數的齒輪三維模型。

3、結論

　　運用UG 進行齒輪精確建模時， 齒廓曲線的數學表達十分重要。借助UG 中的規律曲線功能可以直接生成齒廓曲線，無需對其進行修剪、變換，對齒廓曲線實現了完全參數化設計。由于采用了UG 內部表達式工具，避免了編程處理，通用性比較強。齒輪精確造型設計對齒輪的應力分析、干涉檢驗、數控仿真等都有實際意義。