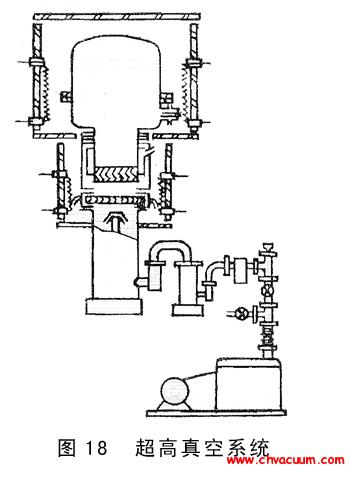
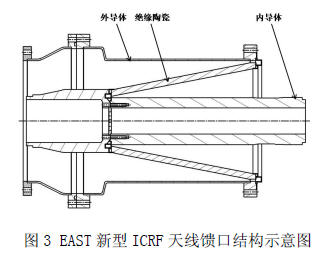
一種真空狀態下的氣體流量測量新方法
當空氣絕對壓力小于40 kPa 時, 目前尚無簡便有效的氣流質量流量測量手段, 為此本文設計了一套新穎的流量標定裝置, 并提出一種了流量測量方法。在流量調節過程中, 調節閥必不可少。真空狀態下, 流經調節閥的流量幾乎完全由閥前、后壓力、氣流溫度四個變量決定。本文由流量標定裝置獲取有效的數據樣本, 基于多元非線性回歸方法建立了流量與四者的關系表達式。一定范圍內只要測定四個變量, 則能直接計算出相應流量。實驗結果表明計算值與實測流量偏差小于3.0%。
真空氣體流量的測量常見于需要真空氣流的過程, 如寬范圍濕度的發生過程, 卷煙的生產過程及大氣環境的模擬過程等。在大氣環境模擬過程中, 動態真空實驗箱內真空環境的更新速度, 是衡量實驗箱性能的一個重要指標。為控制動態真空實驗箱內真空環境的更新速度, 必須實時測量真空狀態下的氣體流量。真空狀態下, 氣體流量的測量具有如下特點 :
(1) 流量密度小, 限制了渦街流量計與超聲流量計的正常使用。對于前者相應的氣流推力過小,對于后者則會產生阻抗匹配的困難。
(2) 不允許引入明顯的壓力損失。真空管道上安裝流量計后增大了阻力, 產生較大的壓損將使動力損耗大大增加, 不利于節能。因而孔板流量計、渦輪流量計、容積式流量計等均不適用。
(3) 流量計在負壓管道上安裝后, 如果存在泄漏很難覺察, 不僅會浪費動力, 而且會嚴重破壞內部氣體環境。
綜上雖然當前關于氣體流量測量的方法多種多樣, 但是基于這些方法設計的流量計一般僅針對非真空( > 100 kPa) 或真空度不高的情形。當氣流絕對壓力小于40 kPa 時, 當前市場上在售的流量計基本上都無法滿足測量要求。在流量調節過程中, 調節閥必不可少。真空狀態下, 氣體通過調節閥的流量主要取決于四個因素, 閥前壓力、閥后壓力、流量系數、氣流溫度。利用調節閥的節流特點, 如果建立起流量與四者的關系模型, 調節閥本身即可以充當流量計, 那么通過測定上述四者的量值, 就可以間接確定真空狀態下的流量。但在建立模型時由于真空狀態( < 40 kPa) 下沒有合適的流量計能夠進行流量測量和標定, 所以無法確定流量值。為此本文基于動態平衡原理設計了一套新穎的流量標定系統,獲取了可靠的數據樣本; 然后利用多元非線性回歸方法與Gauss-Newton 算法對數據進行建模, 確立了流量與四個變量的關系表達式; 基于此表達式只需測定四個變量便能直接計算出相應的流量。
1、 調節閥的節流特性
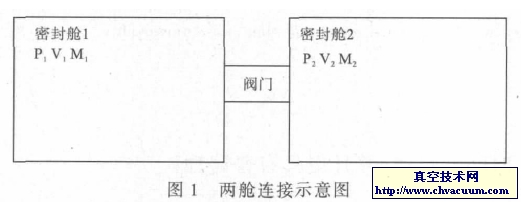
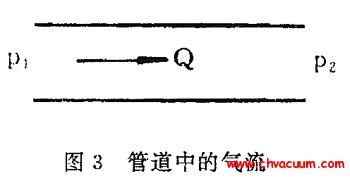
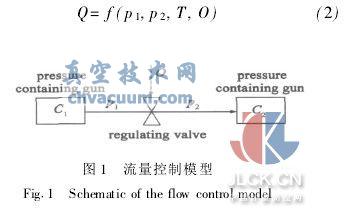
如圖1 所示, 調節閥具有節流特性, 流經調節閥的流量可由式(1) 計算得到
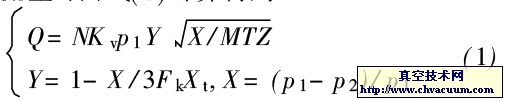
式中,N為考慮到具體單位的數值常量;Kv為調節閥固有流量系數;p1為閥前壓力,p2為閥后壓力;X為壓差比;M為氣體的分子量;T為氣流溫度;Z為壓縮因子,在真空狀態下,其值接近為1;Fk為氣體比熱系數,對于空氣Fk=1;Xt為臨界壓差比,主要取決于閥體的結構。對于可壓縮流體的流動有阻塞流和非阻塞流兩種情形,其判別標準為:若(p1-p2)/p1
從式(1)可知流量的大小主要取決于閥門與流體的物理特性,而且當閥門開度O發生變化時,Kv值也會相應改變。因而流量與閥門開度O、閥門上游壓力p1、下游壓力p2、氣流溫度T的綜合函數關系可以表達為
由式(2)可知,如果能夠獲知流量與四個變量的關系模型,那么就可以通過測量四個變量計算出相應的實際流量。確定關系模型的首要前提是采取一定的方法獲得有關流量與四個變量的有效數據樣本。
2、基于動態平衡的流量標定方法
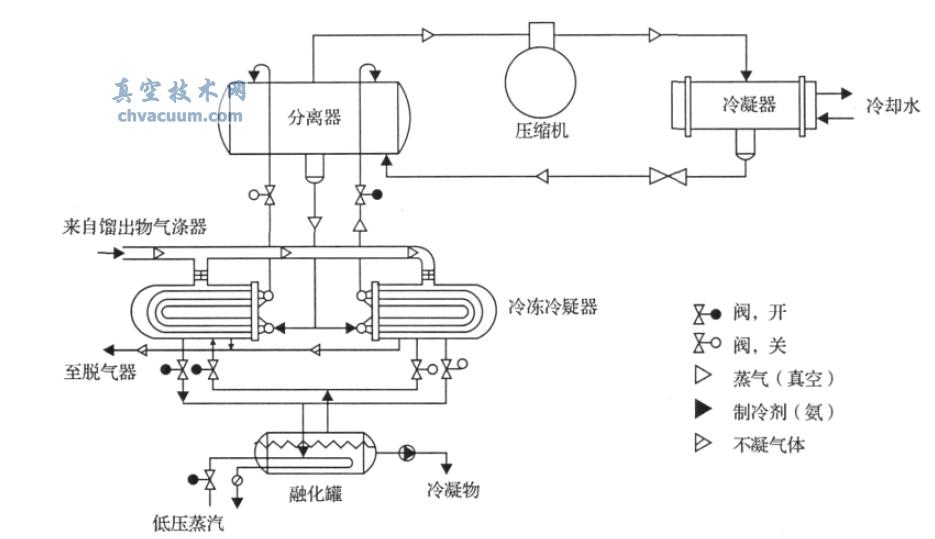
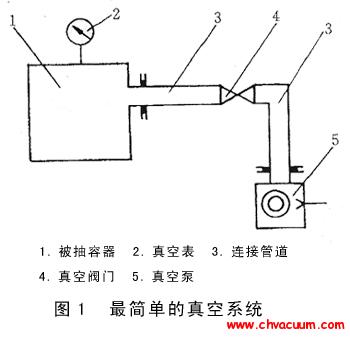
當絕壓小于40 kPa時,目前沒有合適的流量計直接進行空氣流量標定,即式(2)中已知p1,p2,T,O無法測得準確的輸出值Q,故難以對樣本進行有效收集,為解決這一問題本文設計了一套流量標定系統,其結構如圖2所示。利用該系統調節閥V1為任一開度時均能夠實現對容腔C1、C2內真空氣流壓力的獨立控制。當C1、C2內真空壓力到達穩態,系統干路流量處處相等[5]。

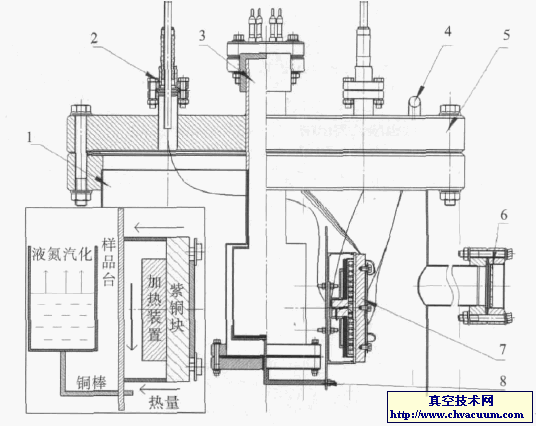
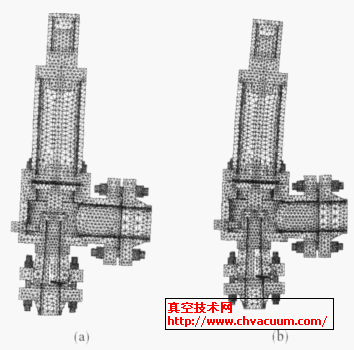
由圖2知流量計安裝在C0與C1之間。控制閥V0、V3安裝在C1的上游,調節C1內的氣流場壓力;控制閥V2、V4安裝在C2的下游,調節C2內的氣流場壓力;控制閥V1充當流量計,在一次流量測定過程中其開度保持不變。假定p0,p1,p2,p3分別為壓力容腔C0,C1,C2,C3內的氣流場壓力。因p0為穩定的氣源壓力,其在實驗過程中始終保持不變。考慮到p1,p2為真空,將p0設定約為100 kPa,從而滿足常規流量計使用條件。當p0,p1,p2,p3均不再變化,整個系統進入動態平衡,流經V1與F1的流量相等,則流量計的讀數即為氣體流經調節閥V1的流量值。流量標定系統的實物裝置如圖3所示。

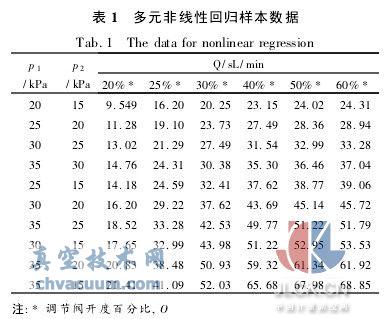
基于上述標定系統,實驗時氣流溫度約20℃,并基本保持不變。試驗獲得66個樣本,其中60個用于表達式系數的回歸分析,其余用作檢驗回歸效果。用于非線性回歸的樣本數據列于表1中。