提出了電子介電常數的計算模型，從不同的角度得到了電子的非相對論散射截面，進一步得到了電子的非相對論性介電常數，發現電子是一色散介質，介電常數是波粒二象性的統一；得到了導體的等效介電常數，驗證了所得電子介電常數的有效性；填補了此項研究的空白。

　　在基本粒子的研究中，電子是一個沒有強相互作用的重要粒子，對其電磁參數、結構的全面研究對物理學及交叉學科的發展有著重要的意義；1897年，英國物理學家湯姆遜第一個用實驗證明電子存在，并測量了電子的荷質比；1907年，密立根利用油滴實驗測量了電子所帶的電量，一個世紀以來，人們普遍認為112電子所帶電荷為1，6×10^-19 庫侖，質量為9.0×10^-31千克，經典半徑約為2.8×10^-15 米；自1973年Kroll和Waston122利用低頻近似公式對低頻電磁場中的電子原子微分散射截面進行計算以來，Geltman等13-82應用不同的方法對激光場中球形粒子、電子原子散射進行了深入的研究。實際上，電子與粒子間的相互作用以及與電磁場的相互作用的研究一直是學術界關注的焦點，然而，用經典理論或量子理論對電子介電常數的研究是一個空白，本文將從經典的電磁理論出發，研究電子的介電常數；具體構成如下:首先從不同的角度給出了電子的非相對論性散射截面，得出了電子介電常數表達式；接著將所得結果用于計算導體的等效介電常數，驗證了所得結果的有效性；最后，給出了本文工作的總結、可能的應用領域及下一步將要開展的研究工作。

1、電子的介電常數

　　1.1、電子的散射截面

　　研究電子的介電常數將涉及到基本粒子的內部結構，是一個根本性的物理問題，需要用量子理論加以研究，在經典的電磁場范圍內，這個問題是不可能完全解決的，所得結果只能用在某些特殊問題上；我們假定電子是一個半徑為R，相對介電常數為Er的均勻介質球，電子的電量均勻的分布于電子的表面；在直到THz的范圍內，電磁波的波長遠大于電子的經典半徑，滿足Rayleigh散射的條件，一般情況下，電子的運動速度v遠小于光速c，相對論效應可以不計1132，因此，可認為靜止散射截面等于運動散射截面；利用解析法192可以得到電子內部的電場：

　　該電場為一均勻電場；電子的散射截面為

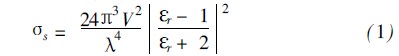
　　其中V為體積，K為電磁波的波長，Er為對介電常數；另外，我們用諧振子作為原子內束縛電子的模型1102，諧振子的固有頻率為X0，電子運動的阻尼力系數為C，在入射電場E0e-jXt的作用下電子運動的微分方程為

3、結論

　　從經典的電磁理論出發，提出了電子介電常數的計算模型，得到了電子的非相對論散射截面，發現在0到THz的范圍內，電子對電磁波的散射符合Rayleigh散射條件；得到了電子的非相對論介電常數，該介電常數是電磁波頻率、電子的經典半徑，電子質量等因素的函數，是波粒二象性的統一反映；將所得結果用于良導體的研究，得到了導體的等效介電常數，通過對其中有關參數大小的分析、計算，發現導體的等效介電常數約為自由空間的介電常數，這一結果與有關文獻一致，驗證了所得電子介電常數的有效性；研究電子的介電常數是一個富有挑戰性的課題，此方面的研究很少看到；對此課題的嚴格解決需要量子理論知識，然而，經典電磁理論所得結果有一定的指導意義，可以把它看成某些情況下的一種平均效應；如何從經典物理出發，進一步得到電子的相對論性介電常數，將是我們下一步要開展的研究工作。