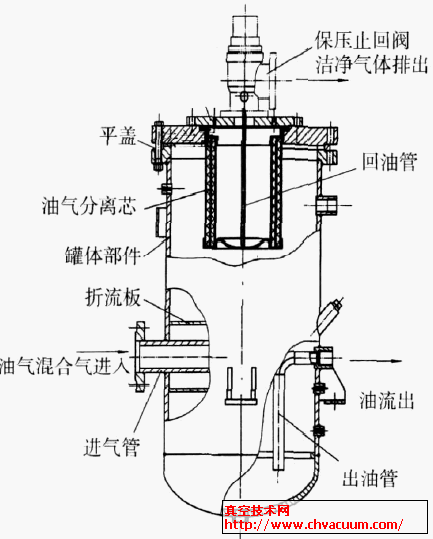
風冷無油渦旋空氣壓縮機換熱計算研究
為了對風冷無油渦旋空氣壓縮機換熱過程進行研究,首先測量了靜盤換熱區(qū)域多個位置的溫度,溫度沿展角和高度方向總體上呈線性變化,受冷卻風的影響,線性分布有所波動,分別用全部溫度數(shù)據(jù)線性擬合和用過內(nèi)端溫度點的線性擬合兩種方式進行處理,計算結(jié)果表明,后者的排氣溫度計算值及變化趨勢與測量結(jié)果更加吻合。把應用范圍更廣、精度更高的Gnielinski 公式用于空氣壓縮過程換熱計算,其中特征長度為渦旋齒內(nèi)壁長度,計算結(jié)果與以往研究中常用的Dittus-Boelter公式基本完全一致,僅換熱系數(shù)變化過程略有不同,對壓縮過程氣體溫度和壓力的變化過程進行了分析。
渦旋壓縮機具有壽命長、運行平穩(wěn)、效率高的優(yōu)點,以制冷劑為壓縮介質(zhì)的空調(diào)渦旋壓縮機或噴水渦旋空氣壓縮機熱力學過程已經(jīng)有了較多的研究,純粹以空氣為壓縮介質(zhì)的風冷無油渦旋空氣壓縮機用于需要清潔氣源的場合,目前相關的研究還不夠深入,缺乏對其換熱過程的研究,B. Blunier和房師毅在忽略壓縮氣體與壁面熱交換的情況下,對無油渦旋空氣壓縮機熱力學過程進行了計算,趙遠揚測試了不同冷卻風量時無油渦旋空氣壓縮機的排氣溫度變化,梁高林研究了雙渦圈無油渦旋空氣壓縮機泄漏線長度隨轉(zhuǎn)角的變化。
空氣的比熱容較小,無油渦旋空氣壓縮機工作過程中溫度較高,熱變形較為嚴重,為了降低對渦旋齒強度的要求,黃英等通過結(jié)構上的改進降低了真空泵壓縮過程中的溫度。無油渦旋空氣壓縮機常用外部風冷散熱的方式降低結(jié)構溫度,渦旋盤的溫度分布與其他渦旋壓縮機有較大的不同,本文通過測量風冷無油渦旋空氣壓縮機渦旋齒上多個位置的溫度,研究了風冷無油渦旋空氣壓縮機渦旋盤換熱區(qū)域的溫度分布規(guī)律,以及渦旋齒溫度數(shù)據(jù)的處理給熱力學計算結(jié)果帶來的影響。把應用范圍更廣、計算精度更高的Gnielinski 換熱系數(shù)準則式用于空氣壓縮過程的換熱計算,其中管長取渦旋齒內(nèi)壁長度,并與以往研究中常用的Dittus-Boelter換熱系數(shù)準則式進行了對比。
1、渦旋壓縮機容腔及排氣過程
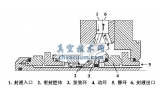
渦旋壓縮機容腔的軸向投影如圖1 所示,按照相互轉(zhuǎn)換關系,分為R-容腔和L-容腔,即吸氣腔LS、RS,第3 壓縮腔LC3、RC3,第2 壓縮腔LC2、RC2,第1壓縮腔LC1、RC1,排氣腔LD、RD,主軸每轉(zhuǎn)動一周,各容腔依次向下轉(zhuǎn)化,排氣腔消失。
為了保證高壓氣體順利排出,減少排氣過程的壓力損失,排氣孔開設較大,主軸轉(zhuǎn)過一定角度后,排氣孔分別與LC1、LD、RD 相通,各容腔排氣面積如圖2 所示,R-容腔和L-容腔的排氣過程并不同步。
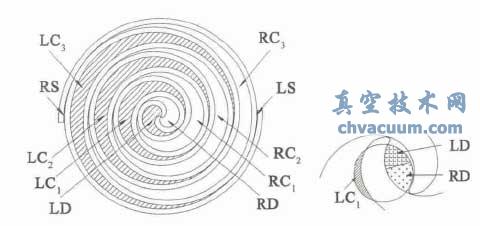
圖1 渦旋壓縮機幾何容腔 圖2 排氣面積
2、渦旋齒溫度測量和數(shù)據(jù)處理
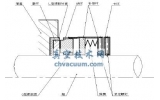
從渦旋齒外端,每π 展角鉆一個測溫孔,用Pt100 熱電阻測量不同轉(zhuǎn)速下渦旋齒的溫度分布,如圖3 所示。當吸氣壓力為0.108 MPa,吸氣溫度為20℃,排氣壓力為0.8 MPa 時,額定轉(zhuǎn)速2900 r /min下的測量結(jié)果如圖4 所示,其它轉(zhuǎn)速下也有著相似的分布規(guī)律。可以看出從齒根到齒頂,溫度與高度基本呈線性關系,沿渦旋齒展開方向,與展角基本上也呈線性關系,換熱計算時可取中間齒高位置的溫度作為渦旋齒溫度,齒根位置相鄰兩測量點的平均溫度作為它們之間底面的溫度。
線性擬合時通常用最小二乘法對所有數(shù)據(jù)點進行計算,考慮到渦旋線內(nèi)端溫度對排氣溫度有直接的影響,強調(diào)內(nèi)端溫度影響時,須使用過渦旋齒內(nèi)端的最小二乘法對其余的數(shù)據(jù)點進行擬合,兩種線性擬合的結(jié)果如圖4(a) 所示。
動靜盤壓縮區(qū)域形狀、外部散熱片形狀和換熱面積基本一致,換熱計算時,假設動盤渦旋齒溫度分布與靜盤相同。
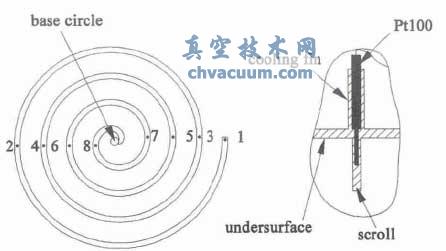
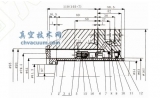
圖3 測溫位置及熱電阻Pt100 的安裝方式
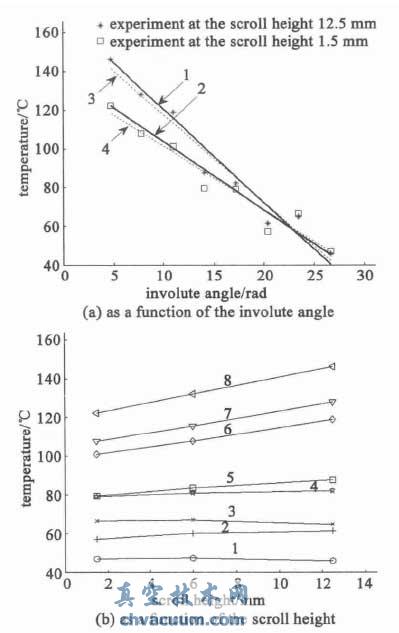
圖4 渦旋齒溫度分布及線性擬合
6、結(jié)論
風冷無油渦旋空氣壓縮機的渦旋齒溫度測量結(jié)果表明,軸向溫差較大,沿展角、高度方向總體上呈線性分布,沿展角的變化過程有所波動,渦旋齒內(nèi)端溫度對排氣溫度影響較大,使用保留渦旋齒內(nèi)端溫度的線性擬合方式,計算結(jié)果與測量結(jié)果吻合較好。特征長度為渦旋齒內(nèi)壁長度的情況下,Gnielinski公式和以往研究中使用的Dittus-Boelter 公式的換熱計算結(jié)果基本完全一致,僅換熱系數(shù)略有不同,由于Gnielinski 公式既可用于過渡流也可用于湍流,且計算精度高,在渦旋壓縮機換熱計算時,可廣泛使用。
吸氣階段結(jié)束到壓縮階段的起始這一時間段內(nèi),氣體由向壁面吸熱轉(zhuǎn)變?yōu)榉艧帷E艢怆A段,LD、RD容腔內(nèi)的氣體向動靜盤底面放熱,被其他壁面加熱。