在動(dòng)態(tài)流量校準(zhǔn)系統(tǒng)中，氣體分子流場(chǎng)分布非均勻性是造成被校規(guī)測(cè)量值出現(xiàn)偏差的原因，也是校準(zhǔn)裝置系統(tǒng)誤差的來(lái)源。介紹校準(zhǔn)室內(nèi)分子流場(chǎng)分布的理論計(jì)算方法，這種方法不僅能分析分子流場(chǎng)分布的非均勻性，還能夠直接計(jì)算被校規(guī)室內(nèi)的分子密度，給出規(guī)室內(nèi)分子密度與進(jìn)入校準(zhǔn)室氣體流量之間的函數(shù)關(guān)系。計(jì)算時(shí)考慮了校準(zhǔn)室的幾何結(jié)構(gòu)，最大限度的減小了校準(zhǔn)室結(jié)構(gòu)設(shè)計(jì)對(duì)分子流場(chǎng)分布帶來(lái)的影響。對(duì)返流比β 和有效抽速Seff的計(jì)算方法，為動(dòng)態(tài)流量校準(zhǔn)裝置系統(tǒng)參數(shù)的蒙特卡羅模擬提供了理論依據(jù)。

1、引言

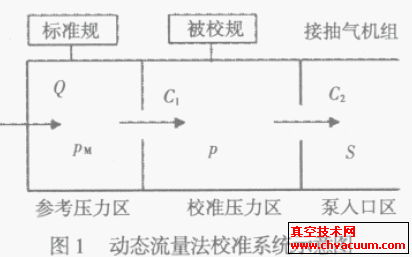
　　動(dòng)態(tài)流量法是將已知流量的氣體連續(xù)的注入到校準(zhǔn)室中，通過(guò)已知流導(dǎo)抽氣，在校準(zhǔn)室中建立起動(dòng)態(tài)平衡壓力。這是運(yùn)用于高真空和超高真空區(qū)間校準(zhǔn)真空規(guī)的一種優(yōu)良的絕對(duì)方法。如圖1 所示。

　　20 世紀(jì)50 年代，隨著擴(kuò)散泵抽速測(cè)量的研究和發(fā)展，對(duì)分子流理論進(jìn)行了深入探討，這為動(dòng)態(tài)流量法的發(fā)展創(chuàng)造了條件。1955 年，Dayton 首先把擴(kuò)散泵抽速測(cè)量裝置進(jìn)行改裝，在擴(kuò)散泵與測(cè)試罩之間裝一限流孔板，建成“小孔法”校準(zhǔn)系統(tǒng)。20 世紀(jì)60 年代，許多國(guó)家相繼建立了不同結(jié)構(gòu)形式的動(dòng)態(tài)流量法校準(zhǔn)系統(tǒng)。隨著真空獲得技術(shù)的進(jìn)展，采用各種優(yōu)良抽氣手段和先進(jìn)工藝的超高真空動(dòng)流量法校準(zhǔn)系統(tǒng)迅速發(fā)展起來(lái),并廣泛而深入的開展了對(duì)誤差源的探討和對(duì)非平衡分子流理論的研究。

　　1960年，Davis首先將蒙特卡羅法應(yīng)用于圓管傳輸幾率的計(jì)算，從此，蒙特卡羅法開始廣泛用于真空計(jì)量領(lǐng)域。Davis 提出了基于蒙特卡羅方法進(jìn)行分子流場(chǎng)分布的基本假設(shè)：校準(zhǔn)室內(nèi)氣體流動(dòng)處于穩(wěn)定狀態(tài)；氣體是分子流，氣體分子之間不發(fā)生碰撞；每個(gè)分子都在它與校準(zhǔn)室內(nèi)壁的碰撞點(diǎn)處被反射；氣體分子飛離器壁時(shí)服從余弦定理；氣體分子在進(jìn)入校準(zhǔn)室入口之前處于平衡態(tài)，進(jìn)入時(shí)的角度分布服從余弦定理。這些假設(shè)已經(jīng)成為對(duì)動(dòng)態(tài)流量校準(zhǔn)系統(tǒng)進(jìn)行蒙特卡羅模擬的基礎(chǔ)。由于當(dāng)時(shí)計(jì)算機(jī)運(yùn)算速度的制約，影響了其深入的應(yīng)用研究。20 世紀(jì)80年代后期，各國(guó)相繼開展了超高真空計(jì)量技術(shù)研究，建立了相應(yīng)的超高真空校準(zhǔn)裝置，有些國(guó)家還建立了極高真空校準(zhǔn)裝置，這對(duì)分子流場(chǎng)分布的深入研究提出了更高的要求。

　　蒙特卡羅方法對(duì)分子流場(chǎng)分布的計(jì)算是通過(guò)模擬大量分子的運(yùn)動(dòng)，跟蹤微觀氣體的運(yùn)動(dòng)（即單個(gè)氣體分子的運(yùn)動(dòng)）來(lái)反映校準(zhǔn)室內(nèi)氣體宏觀參量的性質(zhì)，一般分子流動(dòng)可用分子流率(molecular flow rate)來(lái)表示，即單位時(shí)間內(nèi)通過(guò)單位面積的分子數(shù)。這與蒙特卡羅方法的本質(zhì)吻合。當(dāng)以流量（Pa·m³/s）為單位來(lái)表示氣體的流動(dòng)，即單位時(shí)間內(nèi)通過(guò)的氣體量時(shí)，流量可以轉(zhuǎn)換為分子流率。因?yàn)樵跍囟却_定的條件下，相同的氣體量（Pa·m³）包含相同的氣體分子數(shù)，這與蒙特卡羅方法的本質(zhì)相符。

3、結(jié)論

　　作者介紹的校準(zhǔn)室內(nèi)分子流場(chǎng)分布的理論計(jì)算方法適用于蒙特卡羅方法模擬校準(zhǔn)室分子流場(chǎng)分布，精確計(jì)算校準(zhǔn)室局部空間分子密度以及計(jì)算動(dòng)態(tài)流量校準(zhǔn)裝置系統(tǒng)參數(shù)返流比β 和有效抽速Seff。應(yīng)用該理論方法對(duì)動(dòng)態(tài)流量校準(zhǔn)系統(tǒng)進(jìn)行蒙特卡羅分析，可以鑒別不同動(dòng)態(tài)流量校準(zhǔn)系統(tǒng)之間的微小差別，并研究這些差別的來(lái)源。在真空計(jì)量進(jìn)入超高/極高范圍后，校準(zhǔn)系統(tǒng)局部結(jié)構(gòu)、局部分子流場(chǎng)分布對(duì)整個(gè)校準(zhǔn)系統(tǒng)參數(shù)的影響越來(lái)越明顯。本文介紹的理論計(jì)算方法將為校準(zhǔn)系統(tǒng)局部與整體之間關(guān)系的精確計(jì)算提供理論依據(jù)�；�于該理論計(jì)算方法的蒙特卡羅模擬存在的最大問(wèn)題是過(guò)長(zhǎng)的計(jì)算時(shí)間，這是影響它應(yīng)用的最大障礙。隨著計(jì)算方法的發(fā)展，計(jì)算時(shí)間有望大大縮短。這也會(huì)為更精確的真空計(jì)量研究提供有用的工具。