小型隔膜真空泵橡膠隔膜的ANSYS有限元分析
分析橡膠隔膜在實際工作中的情況,建立隔膜二維軸對稱結(jié)構(gòu)隔膜有限元模型和三維模型,利用ANSYS 有限元分析軟件對隔膜真空泵橡膠隔膜進行分析計算,從理論力學(xué)模型分析計算和實驗驗證兩種方法對仿真分析結(jié)果進行驗證,并利用分析結(jié)果對橡膠隔膜的結(jié)構(gòu)設(shè)計進行優(yōu)化。
隔膜真空泵是一種干式運行、真空度相對不高的真空泵,工作原理是通過往復(fù)拉伸- 壓縮隔膜,造成隔膜室容積發(fā)生變化,再結(jié)合單向閥切換氣路,完成抽取真空的功能。由于橡膠隔膜本身彈性大,對氣體并不能實現(xiàn)完全壓出,故隔膜真空泵的真空度一般不高于200 Pa,但是其具有體積小,重量輕,使用方便等優(yōu)點,所有與氣體接觸的部件經(jīng)過防腐處理后可以完全解決了真空泵的抗化學(xué)腐蝕問題。特別適合用于需要抗化學(xué)腐蝕或需長時間不間斷運行的場合,主要應(yīng)用于食品、化學(xué)、醫(yī)藥、航空和汽車等工業(yè)。橡膠隔膜是隔膜真空泵最關(guān)鍵的部件, 長時間、高真空的使用要求對隔膜的材料和其相關(guān)部件的設(shè)計提出了更高的要求。本文作者使用有限元分析軟件ANSYS 對隔膜真空泵的橡膠隔膜進行建模并分析計算,為優(yōu)化橡膠隔膜的設(shè)計奠定了基礎(chǔ)。
1、橡膠材料的理論基礎(chǔ)及數(shù)據(jù)擬合
隔膜的材料采用的是橡膠,橡膠由于交聯(lián)分子鏈拆開的原因可承受高達100%~700%的彈性變形,人們在研究橡膠材料時,認(rèn)為它是各向同性不可壓縮的超彈性體。橡膠是一種超彈性材料,超彈性材料的本構(gòu)關(guān)系呈現(xiàn)復(fù)雜的非線性。橡膠的泊松比接近(接近0.5)大于塑料(0.3)。一般工程材料的應(yīng)力狀態(tài)可以通過彈塑性曲線來描述,而超彈性材料則是通過彈性勢能函數(shù)來描述,應(yīng)力- 應(yīng)變關(guān)系是高度非線性的。橡膠力學(xué)模型表現(xiàn)為復(fù)雜的材料非線性和幾何非線性。目前,理論模型可以分為兩類,基于熱力學(xué)的動力學(xué)理論高斯統(tǒng)計模型和非高斯統(tǒng)計模型; 基于連續(xù)介質(zhì)力學(xué)的多項式模型,Neo-Hookean、Arruda-Boyce (限于應(yīng)變最多達到300%)、Ogden(可以用于應(yīng)變達700%的情況)模型和Mooney-Rivlin 模型。Neo-Hookean 模型具有常剪切模型,適用于近似預(yù)測30%~40%的單軸拉伸80%~90%的純剪切行為。目前工程上應(yīng)用較多的是2 參數(shù)Mooney-Rivlin 模型(相當(dāng)于1 項多項式模型)。
2、橡膠隔膜的ANSYS 有限元分析
2.1、橡膠隔膜的幾何結(jié)構(gòu)
隔膜真空泵的橡膠隔膜結(jié)構(gòu)如圖3 所示。從圖可以看出此橡膠隔膜為軸對稱結(jié)構(gòu),故分析時只對其截面進行分析。

圖3 雙層橡膠隔膜
2.2、有限元模型的建立
建立橡膠隔膜的軸對稱有限元模型。橡膠隔膜采用Hyper183 單元,橡膠隔膜中心部分實際有一鐵心,實際分析時并不影響,可以舍去后單對隔膜進行研究。橡膠隔膜的截面結(jié)構(gòu)如圖4 所示。
2.3、約束及應(yīng)力加載
橡膠隔膜的位移及應(yīng)力約束如圖5 所示。
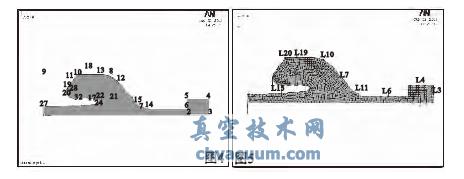
圖4 橡膠隔膜截面圖 圖5 橡膠隔膜位移和應(yīng)力加載
2.3.1、位移邊界條件
(1)隔膜右端上下兩面及右端面被氣室蓋和泵殼壓緊,其各種自由度被限制,如圖所示,其位移將被完全限制;
(2)橡膠隔膜中心部位移將被耦合,隔膜中心部分添加一個位移為5mm 的位移約束;
(3)由于是軸對稱分析,在圖形的最左端還要添加一個軸對稱約束,如圖所示隔膜模型的最左邊。
2.3.2、應(yīng)力邊界條件
(1) 橡膠隔膜的上側(cè)有1 atm 大氣壓的壓力作用,在上表面添加一個方向朝下的大氣壓;
(2) 橡膠隔膜的下側(cè)受到真空吸力的作用,在隔膜下表面添加一個方向朝下的大氣壓。
2.4、計算結(jié)果及分析
由分析結(jié)果可知,橡膠隔膜受力最大的部位位于抽真空面的中部和上端位移被約束處的直角部位,分析結(jié)果與實際零件圖8 的失效形式一致。在此分析結(jié)果和實際試驗的指導(dǎo)下,對橡膠隔膜進行結(jié)構(gòu)優(yōu)化,經(jīng)過優(yōu)化后的隔膜工作壽命遠(yuǎn)遠(yuǎn)超過了3600 h,達到了設(shè)計要求。
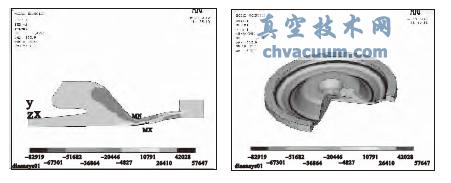
圖6 應(yīng)力圖 圖7 變形圖
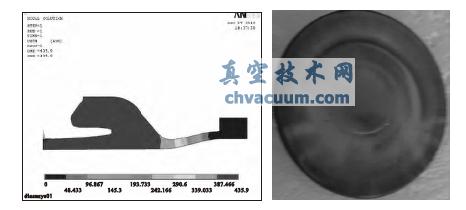
圖8 實際零件圖
3、結(jié)論
本文通過有限元分析的方法對橡膠隔膜進行了力學(xué)分析,并建立其2 參數(shù)的M-R 數(shù)學(xué)模型,得到橡膠隔膜最大應(yīng)力及應(yīng)變情況,為橡膠隔膜和真空氣室的設(shè)計提供了理論依據(jù),本文提出的分析方法同樣適用于其他超彈性體的研究。經(jīng)過研究,得出了以下結(jié)論:
(1) ANSYS 有限元超彈性分析符合實際情況,能夠有效反應(yīng)橡膠的應(yīng)力- 應(yīng)變情況。
(2) 此橡膠隔膜最大應(yīng)力在真空接觸面的中部和上端直角處,為橡膠的優(yōu)化設(shè)計提供了依據(jù),應(yīng)變模型為真空氣室的結(jié)構(gòu)設(shè)計提供了依據(jù)。
(3)分析所得應(yīng)力與實驗所得應(yīng)力相符。