為了提高計算全息圖傳統二值化方法的計算速度，本文提出了一種基于塊的計算全息圖二值化方法。從數值重現和光電重現兩個方面驗證了這種二值化方法的可行性，并與羅曼Ⅲ型編碼重現結果進行比較，比較結果表明對相同尺寸原圖計算其二值化全息圖，本算法耗時僅為羅曼III 型編碼的1/36。然后分析兩種方法各自的優缺點，從理論上解釋了影響重現圖像質量的原因。結果表明，與羅曼編碼相比，本文中提出的二值化方法具有運算快速、準確的優點。

　　全息技術被認為是最終的三維顯示技術，因為它記錄了三維物體所有的視差信息，三維視覺效果逼真。但是由于記錄方法和記錄材質的限制，傳統光學全息并不能實現實時、動態的顯示。上世紀末隨著計算機技術、數字多媒體技術以及顯示技術的發展，計算全息術與空間光調制器（Spatial Light Modulator ,SLM）的結合讓全息視頻成為可能，從而日漸成為研究熱點。

　　計算全息術根據全息的原理，通過編碼方法將物體的衍射光波記錄在一個二維的矩陣中。根據物光波衍射距離的長短和編碼方法的不同，計算全息圖有不同分類。由于物光波只是一個數學上的存在，這個三維物體可以是真實的也可以是虛擬的，因此計算全息術具有獨特的優點和極大的靈活性。但是全息圖巨大的計算容量和空間光調制器分辨率的不足限基金項目：國家高技術研究發展計劃（863 計劃）資助項目（2007AA01Z303）；高等學校學科創新引智計劃基金資助項目（B07027）限制了計算全息技術的發展。目前，針對實時動態全息顯示，一些快速算法被提出。例如麻省理工學院空間成像小組的M. Lucente, 提出的特殊衍射算法（diffraction specific），省略了傳統全息圖計算方法中首先對物光波衍射的計算，運用逆向思維，提出了基本條紋的新概念，大大提高了計算速度。日本千葉大學為了提高運算速度，開發了專用集成電路，讓實時全息距離現實更進了一步。一般情況下計算全息圖可以用三種方式重現：光學重現，數值重現以及光電重現。數值重現和光電重現是本文中實驗的主要方法和手段。光電重現結合了現代顯示技術和計算機技術，將計算得到的二維矩陣轉換為電壓信號，施加在空間光調制器上，達到對參考光進行調制的目的， LCOS 由于其越來越小的像素尺寸和高衍射效率而成為光電重現中光調制器的首選。

　　LCOS 顯示器件通過對入射光偏正方向的調制來達到調制入射光強度的目的，在調制過程中相位并不是一個常數，它隨著輸出灰度級的變化而變化。這就給光電重現帶來制約因素，因為全息圖通常僅僅對入射光振幅或相位進行調制。目前為了解決液晶空間光調制器的相位問題，一般都是將計算得到的全息圖二值化，即處理成灰度等級只有0 和255 的圖片。這樣得到的全息圖因為只有簡單的兩個灰度，因此不存在灰度不同引起的相位差，提高了全息圖的抗干擾能力。

　　為了實現全息圖的二值化，早在1965年羅曼就相繼提出了羅曼Ⅰ，Ⅱ，Ⅲ型編碼，這種編碼方式得到的全息圖本身就是二值化的。羅曼編碼用待記錄的物光波調制全息圖中光柵的形狀和位置而不是全息圖的灰度分布，因此它對像素總數的要求很高，一般空間光調制器1024*768的像素數很難滿足。還有其他的一些編碼，例如Burch編碼中待記錄的物光波調制的是全息圖的灰度分布，直接計算得到的是灰度全息圖，為了能對這樣的全息圖進行光電重現，必須采用專用的二值化方法。目前將灰度全息圖二值化的方法眾多，主要分成兩種：一種是非迭代算法，例如Floyd and Steinberg首先提出而后被Hauck and Bryngdah用于計算全息的誤差擴散算法（error diffusion），每個像素的灰度值二值后產生的誤差需要逐個計算，對計算機的計算速度要求很高。另一種是迭代算法，根據迭代中約束條件的不同，又有很多分類，例如逐步迭代法（interative stepwise）和直接二值搜索法（directbinary search）以及梯度隨機二值法[16]（gradual and random binariation ）。逐步迭代法選擇兩個不同的閾值，每迭代一次按照一定的步長改變閾值，當兩個閾值正好相等時，退出迭代。直接二值搜索法則在每次迭代中只有一個閾值。梯度隨機二值法每次迭代的過程中被二值化的像素是隨機的，而且經過二值處理的像素數目是梯度增加的。迭代法能夠最大限度限制重現圖信息丟失，但是不利于實時顯示。為了降低二值化過程的運算量，本文提出一種非迭代的二值化算法。

　　本文由三部分組成。第一部分介紹羅曼編碼的原理，提出本文的二值化算法。第二部分給出經這種算法二值化后得到的全息圖的數字重現結果以及與羅曼編碼數值重現結果的比較。第三部分給出經這種算法二值化后得到的全息圖的光電重現結果與羅曼Ⅲ型編碼光電重現結果的比較。最后是本文的結論。

1、二值化方法的提出

1.1、羅曼Ⅲ型編碼的二值化原理

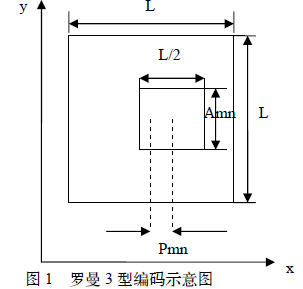
　　羅曼根據不規則光柵的衍射效應，提出了迂回位相編碼技術，根據通光孔的形狀不同產生了3 種羅曼型編碼，即羅曼Ⅰ，Ⅱ，Ⅲ編碼。羅曼Ⅲ編碼相比與其它兩種羅曼型編碼具有精度高的優點，因此本文中選用羅曼Ⅲ型編碼。圖1是羅曼Ⅲ型編碼的示意圖。虛擬全息底片可以視作正方形小單元的組合，每個正方形單元中有一個矩形通光孔，通光孔的寬度一定，一般選擇為L/2。通光孔高度Amn 由待記錄衍射光波Xm,Yn 處的幅值調制，最大為L。因此L 的大小決定可被調制振幅的級數。通光孔的中心到正方形單元中心的偏移量Pmn 由待記錄衍射物光波Xm,Yn 處的相位所調制，L 大小也決定可被調制相位的級數。L越大，振幅和相位可被調制的級數越多，得到的全息圖越精確。在計算中，L 一般取2的整數次方。計算出所有通光孔的位置和大小，進而得到全息圖。這種編碼方式下得到的全息圖采樣點數是物的采樣點數的L*L 倍。羅曼編碼的優點在于能直接得到二值化的全息圖，缺點在于計算量巨大，不能實現實時顯。

1.2、基于塊的二值化方法

　　根據羅曼編碼的編碼原理，計算得到的全息圖的像素數大小將會是物的像素數大小的數倍，要得到計算精確的全息圖對計算機計算容量和計算速度的要求很高，加上空間光調制器像素數目的限制，羅曼編碼在現階段并不適合于三維實時顯示。Burch 編碼雖然計算得到的是灰度全息圖，但是全息圖的像素數目并未增加，因此耗時相對于羅曼編碼大大減少 。因此，先通過Burch 編碼計算灰度全息圖，再用專門的二值化算法進行二值化的方法是可行的。