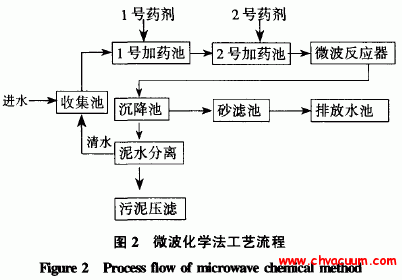
電弧離子鍍于20世紀80年代興起,是物理氣相沉積( Physical Vapor Deposition,PVD) 技術的一個重要分支。基本原理是在真空條件下,靶源作為陰極、殼體作為陽極,利用陰極與陽極之間的弧光放電蒸發并電離靶材,產生等離子體,對樣品進行沉積鍍膜。電弧離子鍍具有沉積速度快、金屬離化率高、膜的附著力強、可鍍材料廣泛等優點,在工具鋼刀具上有廣泛的應用。

　　在電弧離子鍍技術中,影響膜層質量的參數很多,如溫度、靶電流、基片偏壓等。針對用電弧離子鍍制備某種材料薄膜時,通常需要對這些參數采用不同的值進行大量實驗,通過鍍膜參數與膜層性能之間的關系對制備工藝進行優化。在這方面電弧離子鍍與其他薄膜沉積技術的研究方法是相同的。然而另一方面,在電弧離子鍍研究中獲得的工藝參數與膜層性能之間的關系很少象其他薄膜沉積技術,如磁控濺射等那樣,在機理上得到解釋。這使得研究人員對電弧離子鍍微觀過程的理解往往停留在假想層面上,從而使工藝參數的優化具有一定程度的盲目性。

　　造成這種情況的一個主要原因是到目前為止缺乏診斷電弧離子鍍等離子體的有效手段。診斷等離子體參數常用的朗繆爾單探針在應用于電弧離子鍍等離子體參數診斷時,會由于電弧離子鍍等離子體非常高的密度,而使探針在接近電子飽和區時收集到很大的電流,從而使探針紅熱甚至發射電子而不能正常工作。另一方面,由于電弧離子鍍等離子體非常不穩定,使測得的I-V 特性曲線非常不光滑,難以直接被用來分析得出等離子體參數。針對這些題,我們采用雙探針方法,結合大量采樣平均和離散傅里葉變換平滑處理,對診斷電弧離子鍍等離子體進行了嘗試,成功獲得了薄膜制備條件下的平均等離子體密度和電子溫度,從而找到了一種實用有效的診斷電弧離子鍍等離子體的方法。實驗結果有助于研究電弧離子鍍等離子體參數與對薄膜生長影響的規律。

1、等離子體診斷原理

1.1、朗繆爾雙探針原理

　　圖1為雙探針診斷等離子體的示意圖。雙探針由兩個形狀、尺寸、材料相同的金屬電極組成, 探針電路與等離子體不共地。假設一個探針的電流為I₁ ,另一個探針的電流為I₂, I₁ 可以表示為:

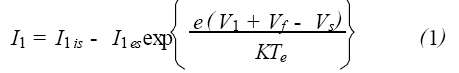
　　其中, I_1is是探針1的飽和離子電流, I _1es是探針2 的飽和電子電流。V₁是探針1 相對于懸浮電位V_f 的電位, V_s 是等離子體空間電位。由懸浮電位的定義式得

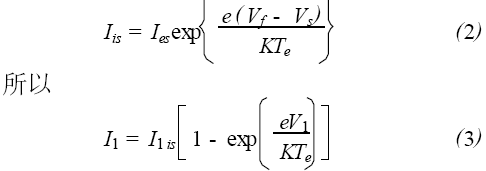
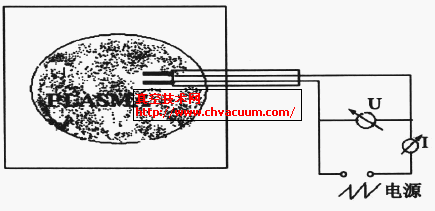
圖1 　雙探針結構示意圖

　　同理,可得探針2的電流表達式為

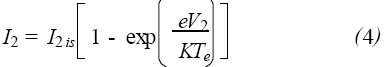
　　I_2is是探針2的飽和離子電流, V₂ 是探針2 相對于V_f 的電位。由于雙探針電路相對于等離子體處于“懸浮”狀態,流入一個探針的電流與流出另一個探針的電流相等,所以I ≡I₁ = - I₂ 。

　　當兩探針完全相同時:

I _1is = I _{2 is} = I_is (5)

　　由式(3)～(5) 得:

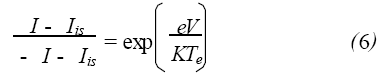
　　V = V₁ - V₂ 是兩探針間的電壓。解等式(6) 得:

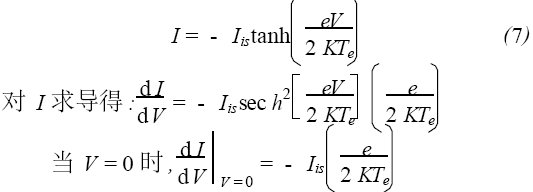
　　由上式可以看出:電子溫度T_e可以用V=0時雙探針特征曲線的斜率求出。

　　由飽和離子電流的定義式得:

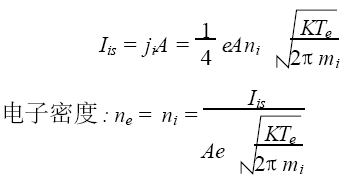
　　其中A 是探針面積, m_i 是離子質量。

　　由公式(7)可以看出,雙探針電流永遠小于離子飽和電流,因此可以避免單探針診斷中出現的由于收集電流過大使探針紅熱甚至發射電子而不能正常工作的問題。

1.2、離散傅里葉變換平滑方法

　　如果用函數f(x) 表示測量數據f(0),f(1), ⋯,f 2N-1)的變化規律,f(x)可以展開成傅里葉級數形式

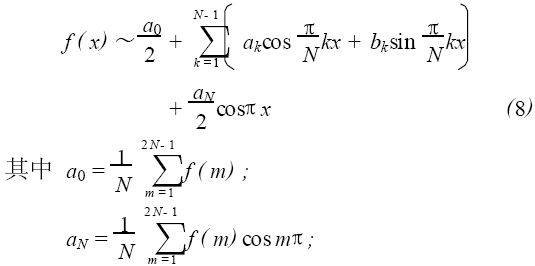
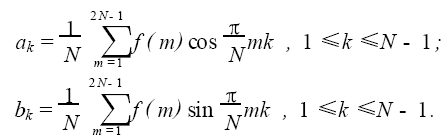
　　把函數f(x)可以寫成如下形式

f(x)= f0(x)+N(x) (1)

　　其中, f0(x)表示測量數據內在的物理規律, N(x)表示噪音成分。可以證明函數越光滑或周期變化的規律性越好,其相應的傅里葉級數收斂越快。由于f0(x)通常是光滑連續的,而噪音N(x)本質上是無規則和不連續的,它們傅里葉展開的收斂性質不同:前者是收斂的,而后者不收斂。基于這種差別,如果在適當的位置( f0(x)已很好地收斂) 把f(x)的傅里葉級數截斷并舍棄高頻項,就可以大幅濾除噪音成分,從而使曲線變得光滑。