為確保電腦等電器設備穩定運行，熱設計是一項很重要的工作。不同海拔高度空氣的密度、壓力等性能下降很多，空氣這些性能的改變對電腦溫度場影響很大。為了能夠準確的計算分析不同海拔高度地區電腦機箱溫度場問題，對風機的性能曲線變化進行了分析研究，對建立在海平面上的主要傳熱數學模型進行了修正，使不同海拔高度溫度場計算更為接近實際情況，為電腦等電器設備溫度場分析設計提供了理論依據。

　　為了使電腦等電器設備在設計的溫度下穩定運行，控制工作溫度不超過設計標準是關鍵。電腦等電器散熱主要是依靠排風扇散熱，其主要散熱形式是對流傳導。不同的海拔高度空氣的密度、空氣的壓力、溫度、空氣粘度等性能會發生很大的變化，海拔越高空氣越稀薄，越接近真空狀態。這些性能的改變會對流傳熱有很大的影響。這就需要建立起海拔高度和電器溫升之間的關系，準確分析計算電腦等電器設備在不同海拔高度的溫度場，研究不同海拔高度傳熱特性，針對不同海拔高度合理進行熱設計，控制電腦等電器設備的溫升，確保其運行安全穩定。

　　多年來，關于電器、手機和電腦等溫度場的熱計方法有很多，其中數值計算方法可靠精度高。國內外的專家學者采用數值計算方法都是針對在海平面和低海拔地區進行的，然而我國的實際情況是水電、風電、石油、煤炭等資源都在高海拔地區，隨著西部能源建設的需要，國內對海拔高度對電氣設備溫升的影響制定了標準，但是相對高海拔地區傳熱研究文獻較少。通常的情況下，測算高海拔電子芯片等電子設備溫升是使用溫升修正系數，這種辦法誤差約在20%以上，精度達不到要求。

　　我國是屬于以高原為主的國家，國土面積有三分之二是1000 m 以上的高原，研究高海拔地區電腦等電器設備溫度場、流場等散熱能力很現實意義。本文以一臺在高海拔地區運行的電腦機箱為研究對象，根據電器設備傳熱理論與高海拔氣體流動特點，對茹卡烏斯數學模型和Chilton-colburn 等典型傳熱模型進行了修正，通過對雷諾數和傳熱系數等熱力學參數進行了完善，建立電腦機箱三維流體場與溫度場耦合求解的數學模型與物理模型。在此基礎上，結合電腦在平原地區的實驗值和海拔高度對電腦溫升的影響，建立了高海拔地區電器傳熱計算理論，對電腦在海平面和海拔4 km 兩種海拔高度運行時的溫升進行了實際計算，并將計算值和ANSYS14.0 仿真結果進行對比分析，證明了修正后的數學模型是準確實用性。為高海拔地區電器的熱設計提供理論計算依據和參考。

　　1、實驗模型和邊界條件

　　1.1、實驗模型

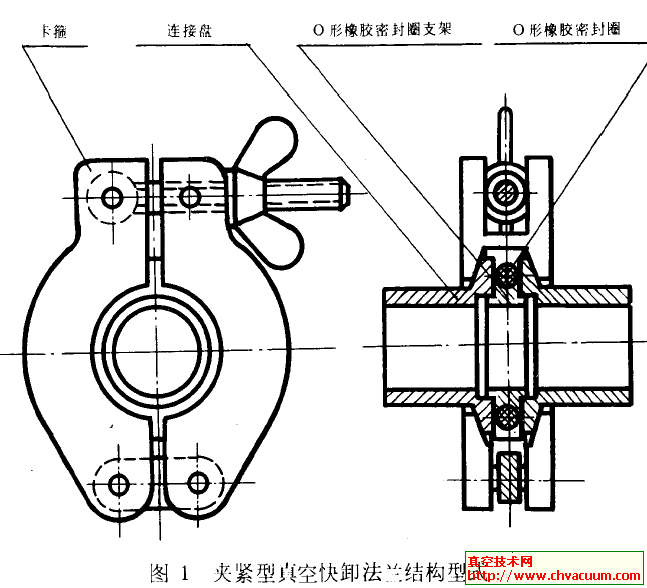
　　由6個零件組成的分析實驗模型，如圖1 所示該模型屬于系統級( 電腦機箱、機柜等) 電子封裝。電腦等電器散熱的方法主要有兩種形式，一是加裝排風扇對發熱電子元件進行強制對流散熱；二是使用散熱器和IC 芯片等發熱量較大的電子器件相連接，以傳導方式進行散熱。模型中鋁制散熱器散熱翅片Z 方向和X 方向都是6組，翅片形狀為圓形，直徑(D) 為20mm，散熱翅片采用順排方式。橫向間距(St) 為30mm，縱向間距(Sl) 為60 mm。PCB板的厚度是12mm，材料為FR-4，導熱系數是0.35W/m·K。鋁制散熱器的導熱系數是205W/m·K。對流風扇轉速恒定，風扇的特性曲線是非線性的，風扇的體積流量由自定義的曲線來確定，隨海拔高度的變化，空氣的壓力、密度等空氣性質發生變化，該特性曲線也隨之發生變化。該系統級模型還有一個用于散熱的百葉窗，這里設定其打開率為50%。在散熱器下面有一個500W 的電子芯片熱源。該機箱為封閉狀態。

表1 不同海拔高度空氣性能

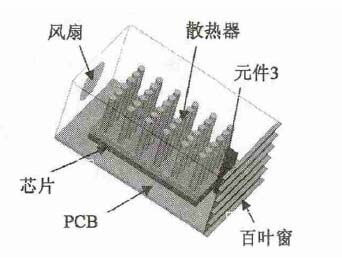
圖1 仿真模型示意圖

　　1.2、邊界條件

　　實驗模型的基本尺寸和翅片形狀、翅片的排列方式都確定下來了，這是分析計算溫度場的基礎。對該模型傳熱分析假設為穩態條件，熱輻射忽略。傳熱介質(空氣) 性質如表1 所示。表中空氣的密度、空氣壓力和空氣的粘度等參數作為機箱熱溫度場分析計算的邊界條件。從表中可以看出，不同海拔高度空氣性能變化很大，如海拔4000 m 時，空氣分子的密度僅僅是海平面的66.8%；大氣壓力是海平面的60%，運動粘度也大大的降低，傳熱介質這些參數對以對流散熱的電子產品來說有很大影響。所以，對不同海拔熱傳計算時，一定要考慮這些變化，這樣確定的邊界條件才真的接近實際數據，溫度場分析計算的結果才準確。

　　如圖1 的系統模型所示，在各元器件功率不變、各尺寸不變的情況下，分別在海平面和海拔高度在4000 m 兩種情況，進行熱分析計算，分別采用理論計算和仿真實驗對比。

　　圖2 所示是在海平面上的風扇工作的特性曲線。海拔高度越高，空氣壓力越小，空氣密度降低，風扇的工作特性曲線也發生變化。高海拔散熱風扇通常有兩種，一種是高度補償型的，這種型式的風扇通常在航空器上使用。另一種是轉速恒定型的，是電器設備上常使用的。

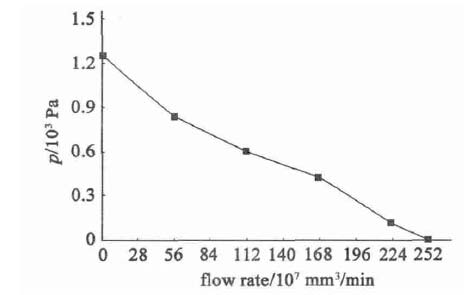
圖2 風扇風流特性曲線(海平面)

　　4、結論

　　分析了不同海拔高度流場傳熱特點，通過引入海拔高度參數，對不同海拔高度空氣密度等性能進行了修正，對雷諾系數等傳熱參數進行了修正，對典型的對流傳導公式進行了修正，最后建立起來了不同海拔高度電腦機箱流場、溫度場計算模型。根據所建實驗模型的尺寸和特點，應用了本文提出的傳熱數學模型進行了分析計算，并在相同邊界條件下，進行了仿真對比研究，其結論如下：

　　(1) 使用本文提出的不同海拔高度傳熱計算數學模型合理正確，進行電腦等電器熱設計時可以實現參數化溫度場分析計算。

　　(2) 較為詳細的分析研究了不同海拔高度空氣的密度、空氣的運動粘度、環境溫度等參數對電腦等電器設備散熱的影響。對電腦等電器設備熱設計時一定要考慮海拔高的影響，才能保證電器設備運行時，工作溫度不超過設計標準，實現電器設備的穩定運行。

　　(3) 使用修正了的傳熱計算數學模型，提高了電腦等電器設備高海拔高度環境下運行時的溫升的計算精度。

　　(4) 高海拔地區空氣壓力、空氣密度等下降，風扇的特性曲線變化很大，風扇散熱能力降低，高海拔地區電器運行溫度比海平面運行溫度高很多，在電器熱設計時，一定要考慮這一因素。