真空泵爪形轉(zhuǎn)子的平衡方法研究
用去除材料的方法對爪式轉(zhuǎn)子做平衡分析,利用平衡理論計(jì)算得出待移除的質(zhì)量m 和待移除質(zhì)量m 在轉(zhuǎn)子上的分布位置A(x, y, z)。然后借助Pro/Engineer、Adams 等仿真工具對去除質(zhì)量后的轉(zhuǎn)子進(jìn)行平衡的模擬仿真,得到模擬的平衡結(jié)果。傳統(tǒng)的平衡方法是將轉(zhuǎn)子放到平衡機(jī)上,用試探性的方法去除材料,然后來驗(yàn)證平衡效果,這樣要反復(fù)實(shí)驗(yàn)才能得到滿意的結(jié)果。將仿真結(jié)果和直接在平衡機(jī)上做的平衡效果進(jìn)行比較,結(jié)果表明:前者平衡效果比后者好,從實(shí)際的操作角度來說,前者一步到位,不用反復(fù)試驗(yàn),節(jié)省時(shí)間。
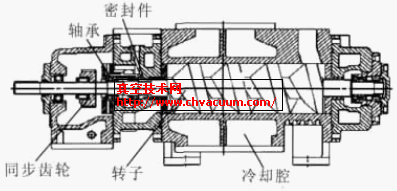
爪式轉(zhuǎn)子無油真空泵,是一種性能優(yōu)良的干式真空泵,它可代替?zhèn)鹘y(tǒng)的油封機(jī)械泵。現(xiàn)已在石油、化工、制藥、食品加工、電子、半導(dǎo)體、航空航天、核工業(yè)等領(lǐng)域得到廣泛應(yīng)用。而爪式轉(zhuǎn)子,作為無油干式真空泵的核心部件,其各個(gè)方面的精度直接影響著干式真空泵的工作效率和工作的穩(wěn)定性。這其中最為關(guān)鍵的技術(shù)之一就是爪形轉(zhuǎn)子的如何平衡問題。做好轉(zhuǎn)子的平衡,可以減輕工作時(shí)軸對軸承的壓力,從而增加軸承壽命。減輕傳動(dòng)齒輪之間的相互摩擦,增加工作效率。
1、平衡理論分析
1.1、轉(zhuǎn)子不平衡的原因分析
由于設(shè)計(jì)、結(jié)構(gòu)、材質(zhì)不均勻、形狀不規(guī)則及制造安裝誤差等原因,所有實(shí)際轉(zhuǎn)子的中心慣性主軸都會(huì)偏離其旋轉(zhuǎn)軸線,這樣,當(dāng)轉(zhuǎn)子轉(zhuǎn)動(dòng)時(shí),轉(zhuǎn)子各微元慣性力所組成的力系不是一個(gè)平衡力系,這就是我們常說的轉(zhuǎn)子的不平衡。設(shè)有一爪形轉(zhuǎn)子,質(zhì)量為m,以等角度ω 繞一固定軸旋轉(zhuǎn),取其轉(zhuǎn)軸上任意一點(diǎn)o 作為坐標(biāo)原點(diǎn),轉(zhuǎn)軸為z 軸,并作出相應(yīng)的ox 及oy 軸,轉(zhuǎn)子質(zhì)心坐標(biāo)為C(xc,yc,zc),質(zhì)心C 對旋轉(zhuǎn)軸z 的矢徑為rc,轉(zhuǎn)子中任意質(zhì)點(diǎn)坐標(biāo)為mi ( xi,yi,zi)對轉(zhuǎn)軸的矢徑為ri,則由理論力學(xué)知識可知,該慣性力系向坐標(biāo)原點(diǎn)o 簡化,可以得到一主矢Ro和主矩Mo。主矢和主矩的計(jì)算公式為:

式中,F(xiàn)i 為質(zhì)點(diǎn)mi 產(chǎn)生的離心力, 大小為miriω2,其指向離心方向,為矢徑ri 的方向,故
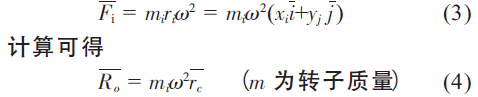
簡化的主矢Ro 的大小與方向和轉(zhuǎn)子質(zhì)心的離心慣性力相等,只不過作用于o 點(diǎn)即Ro//rc,其大小與方向和簡化中心o 點(diǎn)的位置無關(guān)而慣性力系向o 點(diǎn)簡化的主矩可寫為
![]()
式中,Mx,My 及Mz 為主矩Mo 在坐標(biāo)軸上的投影,其大小等于力系所有各力對該軸之矩的代數(shù)和,它們都和o 點(diǎn)的位置無關(guān)。

由以上分析可知,轉(zhuǎn)子的慣性力向任一點(diǎn)簡化的結(jié)果一般得到一個(gè)力和一個(gè)力矩。轉(zhuǎn)子在旋轉(zhuǎn)時(shí),主矢和主矩方向都在變化,其矢量隨同轉(zhuǎn)子一同旋轉(zhuǎn)成為引起軸承振動(dòng)的激發(fā)源。所以,轉(zhuǎn)子平衡的充分必要條件就是:慣性力系向任一點(diǎn)簡化的主矢和主矩都為零,即
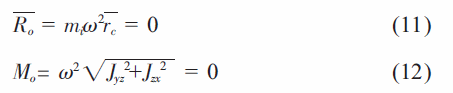
由Ro= 0,則rc= 0,這說明旋轉(zhuǎn)軸必定通過質(zhì)心C;由Mo=0,則Jyz+Jzx=0,滿足條件的轉(zhuǎn)軸z 成為慣性主軸,通過質(zhì)心的慣性主軸成為中心慣性主軸。因此,要消除轉(zhuǎn)子對軸承的動(dòng)壓力只需旋轉(zhuǎn)軸是中心慣性主軸。由于爪形轉(zhuǎn)子形狀不規(guī)則,因此其對旋轉(zhuǎn)軸為中心的質(zhì)量分布不對稱。所以,爪形轉(zhuǎn)子大都是不平衡的。要使一個(gè)不平衡的爪形轉(zhuǎn)子變?yōu)槠胶廪D(zhuǎn)子,就要重新調(diào)整轉(zhuǎn)子的質(zhì)量分布,即在其某個(gè)部位加重或者去重,使轉(zhuǎn)子的中心慣性主軸和旋轉(zhuǎn)軸一致。這時(shí),其慣性力系能夠滿足(11)和(12)式,轉(zhuǎn)子成為平衡轉(zhuǎn)子。
1.2、質(zhì)量代換的質(zhì)量劃分方法
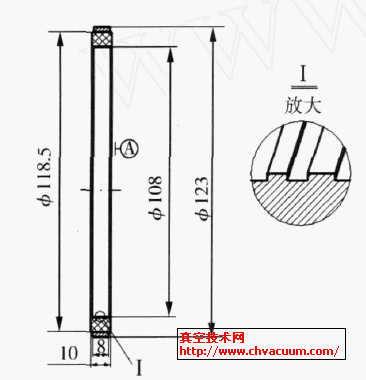
爪型轉(zhuǎn)子的理論型線為ABCDEFGHA 組成的輪廓,由6 段曲線組成。
第1 段:曲線AB 與另一轉(zhuǎn)子上的對應(yīng)點(diǎn)F共軛,為一段擺線。
第2 段:曲線BC 與另一轉(zhuǎn)子上的對應(yīng)圓弧EF 共軛,為一段圓弧。
第3 段:曲線CDE 與另一轉(zhuǎn)子上的對應(yīng)點(diǎn)E共軛,為一段擺線。
第4 段:曲線EF 與另一轉(zhuǎn)子上的對應(yīng)圓弧BC 共軛,為一段圓弧。
第5 段:曲線FG 與另一轉(zhuǎn)子上的對應(yīng)點(diǎn)A共軛,為一段擺線。
第6 段:曲線AHG 與另一轉(zhuǎn)子上的對應(yīng)圓弧AHG 作純滾動(dòng)。
具體的轉(zhuǎn)子型線輪廓,如圖1 所示。
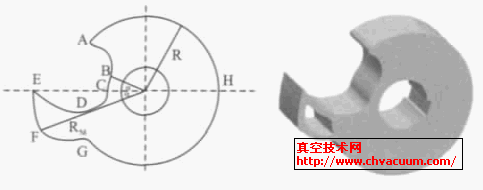
圖1 爪形轉(zhuǎn)子的理論型線 圖2 面積拆分示意圖
從上面的分析我們可以知道,轉(zhuǎn)子型線并非規(guī)則的對稱圖形,所以質(zhì)心并不在其旋轉(zhuǎn)軸心,從而不能正常工作,我們需要將轉(zhuǎn)子部分質(zhì)量移除,以達(dá)到平衡的目的。移除質(zhì)量時(shí)我們用到了質(zhì)量代換法這種方法就是將構(gòu)件用若干集中質(zhì)量來代換,使這些代換質(zhì)量與原質(zhì)量在動(dòng)力學(xué)上等效。具體的代換條件有如下,
(1)代替前后構(gòu)件的質(zhì)量不變
![]()
(2)代替前后構(gòu)件的質(zhì)心位置不變

(3)代替前后構(gòu)件對質(zhì)心軸的轉(zhuǎn)動(dòng)慣量不變
![]()
注:其中構(gòu)件質(zhì)量、質(zhì)心位置、對質(zhì)心轉(zhuǎn)動(dòng)慣量分別為m、s、Js。