首先使用有限元分析方法求解磁控濺射電磁場的分布，然后結合受力分析，仿真了單電子運動軌跡并較好地呈現螺旋形狀，同時模擬出多粒子束的靶面位置分布以及刻蝕形貌圖，最后把計算結果與實驗中靶面刻蝕形貌進行對比，所求結果與實驗測量數據吻合。

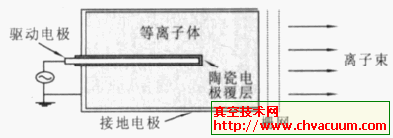
　　在各種濺射鍍膜技術中，磁控濺射技術是最重要的技術之一，它在等離子體產生、維持以及效率方面與其他技術相比都有了很大的改進，較易獲得高的沉積速率，致密性與結合力更好的薄膜，因此在機械、光學和電子行業得到了廣泛的應用。近些年來，關于磁控放電的理論得到廣泛的研究，主要包括磁場結構的分析以及物理機制討論。在磁場放電區域，電子被限制在磁力線平行于陰極表面的位置，從而產生出高電離化的背景氣體。在這個區域產生的離子被加速運動的過程中，又會受到電子和離子的碰撞同時產生出二次電子來維持放電。在磁控濺射系統中，由于特殊的磁場結構，靶材表面的磁場分布以及離子分布是不均勻的，從而導致刻蝕的不均勻性，這對于靶的利用率是一個極大的限制，因此針對于靶面粒子分布以及刻蝕形貌的研究具有很重要的指導意義，而最有效的方法就是通過計算機建立模型仿真。

1、計算方法

1.1、電磁場分布的計算

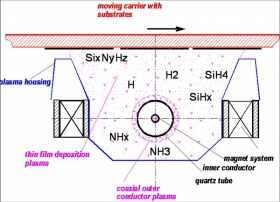
　　平面磁控濺射系統結構如圖1所示，圖中靶基距為30mm，陰極加-300V偏壓，陽極接地，選取鋁為靶材，直徑為100mm，濺射氣體選擇氬氣。為模擬靶材上方X 與Y 方向的磁場分布以及Y 方向的電場分布，利用有限元分析軟件ANSYS 針對上述模型進行求解。磁場與電場分別由公式（1）和（2）表示

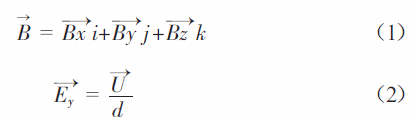
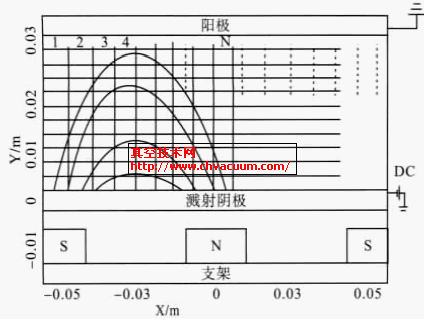
圖1 平面磁控濺射示意圖

1.2、單電子運動的模擬

　　設粒子的電荷為q，運動速度可以表示為：

　　粒子受到電場力和磁場對它的洛倫茲力的共同作，滿足運動方程（4）

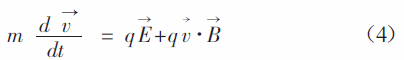
　　速度可以通過上式進行求解，位移表示成方程組（5~7）

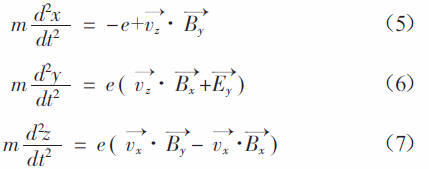
1.3、靶面粒子束流的分布

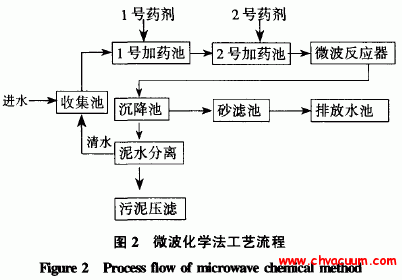
　　對粒子分布的求解算法如圖2 所示。針對電子，首先從X=[-50mm，50mm]，Y=[-30mm，30mm]的區域內任意選定N 個電子，通過前面的電磁場分布可以得到每個電子受到的電場力與磁場力，判斷如果電子在所規定的區域內部，則開始運行程序，設定時間步長dt，計算電子在每個時間步長內三個坐標方向上速度與位移的改變量，判斷位移改變是否大于電子運動的平均自由程λ，電子自由程指電子在兩次碰撞之間運動的平均距離。假設氣體層的厚度是dx，密度為n，r表示氣體原子的半徑，單成分氣體中，平均自由程表示為

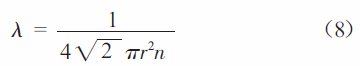
　　如果位移改變大于λ，則有碰撞發生，碰撞后粒子的能量由公式（9）表示

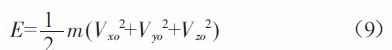
　　此時如果不產生新電子，碰撞為彈性碰撞，滿足動量守恒定理；如果產生新電子，碰撞為非彈性碰撞。新電子速度大小和方向服從隨機數分布，生成隨機數C=rand[0,1]，三個方向的速度大小如公式（10~12）所示

　　最后把電子經過dt時間的運動后的位置分布圖繪制出來，對于離子分布的求解與電子算法相同，只是離子受到的電場力方向與電子相反，在這里就不具體陳述了。

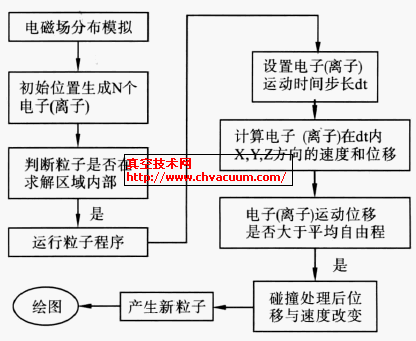
圖2 粒子分布算法

1.4、靶面刻蝕形貌

　　如圖1 所示，將靶材表面區域內的磁場從起點沿靶材的水平和豎直方向劃分為N*N 個網格。將靶材表面第i 個等分點處的疏密程度映射為濺射坑的深度Depth(i)

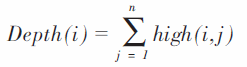
　　其中，high (i,j) 為P 點與靶材間的距離，n為第i個等分點處磁力線的條數。