基于分形理論，描述了玻璃纖維多孔介質材料微尺度空間結構，建立分形等效單元體模型，分析了影響其真空下有效導熱系數關鍵因素為固體基質導熱系數、空隙率、纖維絲空間結構、分形直徑、殘余氣體壓力及導熱系數、玻璃纖維材料厚度、使用環境等，并導出了氣相、固相熱傳導計算公式和熱輻射等效導熱系數計算公式及材料總有效導熱系數計算公式。研究表明，玻璃纖維有效導熱系數隨著分形直徑、分形維數、殘余氣體壓力的增大而增大，隨著空隙率的增大而減小。同時,模型計算值與實驗測量值比較，具有較好的一致性。文章的分析方法對新型真空絕熱材料的研制和絕熱性能的提高具有實用價值。

　　玻璃纖維作為一種典型的保溫多孔介質材料,因其質輕、絕緣性好、耐熱性強、抗腐蝕性好、機械強度高，廣泛應用于家電、交通運輸、土木建筑等國民經濟領域。玻璃纖維作為真空絕熱板的理想芯材之一，目前已被國內外諸多生產企業作為首選。關于纖維絲多孔介質保溫性能的評估，國內外學者也展開了相關理論研究，并建立了諸多物理及數學模型。但其內部結構極其復雜，影響導熱系數的物性參數很多，宏觀角度難以反映其真實情況，并得出接近真實值的結果。從微觀角度出發，J. G.Pharoah 等建立了相應的微尺度空間模型，尤其是Moran Wang建立了Latt ice Boltzmann 的微尺度空間模型，分別介紹了玻璃纖維導熱系數的影響因素，分析了玻璃纖維絲的內部排布格局，纖維絲的平均直徑等對導熱系數的影響，但對其真空下的導熱系數研究并未涉足。中國溫永剛等對2~ 5 um 的玻璃纖維真空絕熱板真空度對其導熱系數的影響進行了實驗研究，得出玻璃纖維內部真空度在50 Pa 以下時其導熱系數低于0.00442 W/ ( m.K) 的結論，但并沒有分析其內部構造對導熱系數造成的影響。

　　將分形理論引入到玻璃纖維多孔介質材料導熱系數的預測和研究，為其熱工性能研究開辟了一條全新的途徑。分形是美國哈佛大學Mandelbrot 教授于1975 年首先提出的，pitchumani、郁伯銘、施明恒等在利用分形理論對顆粒狀多孔介質有效導熱系數進行了深入的研究，并推導出相應的數學表達式。闞安康曾采用分形理論研究了泡沫多孔介質有效導熱系數的方法。Razani和Krishnan以Sierpinski 毯為概念模型提出了空隙分布的理論模型。但這些模型和數學表達式涉及的分形維數及計算方法較為復雜。馬永亭等根據分形理論推導出多孔介質有效導熱率數學模型，該模型表明多孔介質的導熱系數是空隙率、面積比、各組分導熱系數之比及接觸熱阻的函數，計算公式中不含經驗常數，且參數較少，計算簡便，但因多孔介質內部分形特征存在差異，其接觸熱阻的確定是相當困難的，該數學模型的通用性還需要進一步驗證。故而，建立一個通用的多孔介質有效導熱系數理論計算模型是相當困難，也是不切合實際的。因此，針對某一種多孔介質，推導出反映其內部結構特征的導熱系數計算模型，是多孔介質研究領域的一個重要發展方向。

　　本文引入分形理論對纖維多孔介質微尺度空間結構進行研究，構建相應的分形物理模型，并分析影響其導熱系數的關鍵因素，推導出結合微尺度空間的理論計算公式，并就其關鍵影響因素進行了計算和討論。

1、纖維多孔介質微尺度空間結構及分形描述

1.1、微尺度空間結構

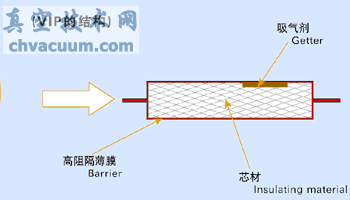
　　作為保溫材料的纖維多孔介質主要是由纖細的纖維絲及纖維絲固體之間的空隙組成，纖維絲層疊交織，阡陌縱橫，空隙連通，空氣在其間可自由流動。就其內結構而言，纖維絲粗細懸殊，布局凌亂，層次錯綜。圖1 所示為掃描電鏡(SEM) 拍攝的玻璃纖維多孔介質芯材微尺度空間結構圖。從圖中可以看到，玻璃纖維絲呈細長圓柱體結構，粗者在20um 以上，細者不足0.1um。玻璃纖維絲縱橫交錯，互相疊壓，玻璃纖維的直徑多集中在2~ 10um 之間，在空間結構上連續分布，具有分形特征。

圖1 玻璃纖維多孔介質芯材微尺度空間實物圖

結論

　　玻璃纖維多孔介質的有效導熱系數不僅與材料固體基質性能有關，還與其內部微尺度空間結構、使用環境溫度等因素有關，從計算結果可以看出，常溫狀態時，綜合有效導熱系數中，熱傳導導熱系數占主導地位，熱輻射有效導熱系數受到溫度影響存在微小波動，但常溫下不占優勢。在使用玻璃纖維作為下，采用增大空隙率等措施提高其整體絕熱性能。

　　從本文分析可看出，采用分形理論建立的數學模型進行玻璃纖維真空下導熱系數的預測，其理論計算結果在高真空狀態下與實驗測量值之間的差異較小，該分形理論模型能真實反應出真空下玻璃纖維真空絕熱熱工特性。通過實驗測試與理論計算對比，經分形理論建立的等效模型與實驗數據走勢具有較好吻合，本模型能反應多孔介質真空下導熱系數與多孔介質微尺度空間結構和板內氣壓之間的函數關系。采用分形理論分析玻璃纖維時，建立其物性與內部微尺度空間結構之間的聯系，這對從理論上提高多孔介質絕熱性能、研制新型環保節能材料等具有重要參考價值。