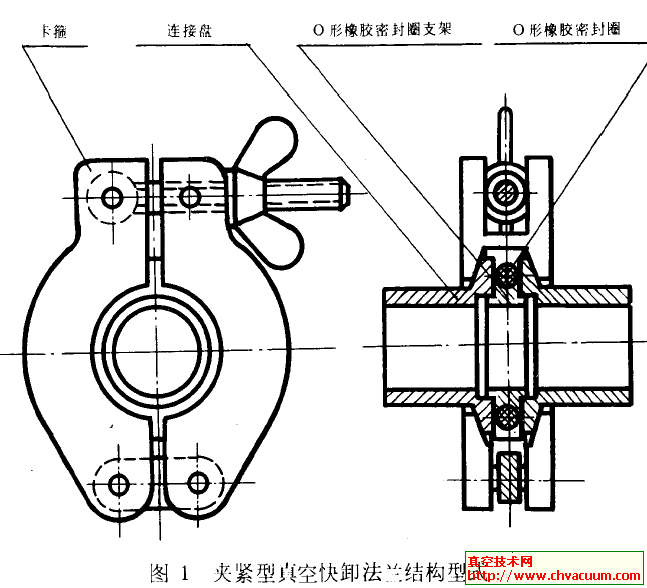
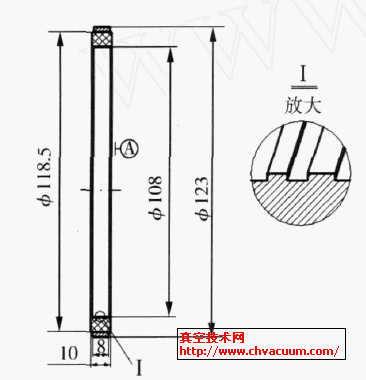
過模波導定向耦合器設計的探討
提出了不同模式進行耦合時,對場分量幅值系數進行歸一化的方法,從而實現了過模波導定向耦合器的設計。仿真模擬驗證了利用該方法進行設計的可行性。
H.A.Bethe的小孔衍射理論是涉及小孔耦合的所有波導元件,定向耦合器、選模耦合器、取樣耦合器、各種小孔激勵裝置等等的計算基礎,R.E.Collin進而提出了小孔耦合定向耦合器的設計方法。但是,Collin方法是基于進行耦合的主、付波導種類、尺寸和模式都相同的前提下建立的,這對常規定向耦合器來說一般都是成立的,而在高功率微波系統中,為了提高波導傳輸的功率容量,普遍使用過模波導,這就使得在這類系統中的定向耦合器主、付波導不同,主波導都是過模波導,而且以圓波導為多,而付波導則一般采用基波矩形波導,以便于與測試儀器連接,進行波形、功率、頻譜、頻率等的測量。顯然,這時的定向耦合器,不僅主、付波導的類型、尺寸不同,而且傳輸模式也不同,這就使得Collin的設計方法不再能直接應用于過模波導定向耦合器的設計。
1、過模波導定向耦合器設計基礎
定向耦合器最主要的參量耦合度的計算,涉及到主、付波導中的功率大小:

式中,P1為主波導中的入射波功率,P+2為在付波導中激勵起來的正向傳輸波的功率。如果主、付波導相同,模式相同,則主、付波導中傳輸的模式波場分量表達式也就相同,它們的功率比就可以直接用幅值比代替,式(1)就可以簡化成
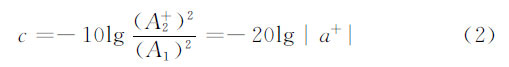
式中,A1為入射波的幅值,A+2為在付波導中正向傳播的被激勵波的幅值,a+ 為主波導入射波與付波導正向激勵波之間的耦合強度。這一計算式就是常見的定向耦合器設計方法的基礎。
但如果主、付波導類型、模式不同,則它們中的場表達式也就不同,它們的幅值系數就不具有可比性,因此式(2)不再適用于過模系統。為此,我們可以在等功率條件下來求出兩個不同模式各自的幅值系數,使之獲得可直接相比的幅值。令
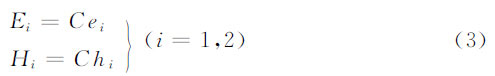
式中,C為場分量的幅值系數,由于場分量的表達式可以寫成不同的形式,因此即使對同一i模式,C 也可以是不同的。ei、hi為場的分布函數。i=1時表示主波導中的入射模式,i=2時表示付波導中的被激勵模式。
3、設計結果
不考慮方向性的優劣,取主波導R =14mm,付波導為標準矩形波導a×b=7.112×3.556mm2,耦合孔厚度t=0.1mm,給定耦合度為60dB,在f=35GHz頻率上計算耦合孔半徑r0以及耦合度的頻率特性。
計算得到的r0 =0.581mm,在此r0值下,改變頻率f,就可以得到不同頻率對應的隔離度與耦合度。為了驗證計算結果的正確性,在以上尺寸下進行了仿真模擬,模擬結果與計算結果如圖2所示。可見,計算與模擬結果良好吻合,證明我們提出的過模波導小孔耦合的設計考慮是正確的。
因為只是為了驗證提出的方法的可行性,因此只舉了一個最簡單的例子,實際的定向耦合器絕大多數是多孔的,關于多孔定向耦合器的設計,已由文獻給出,這里不再進行討論。
本文提出的方法僅為作者的初步考慮,提出來供大家探討。